Рассмотрим на примере порядок построения эпюр при поперечном изгибе (рис. 5.4).
Пример.Дано: 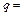 1 т/м;
1 т/м; 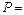 2 т;
2 т; 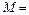 2 т·м.
2 т·м.

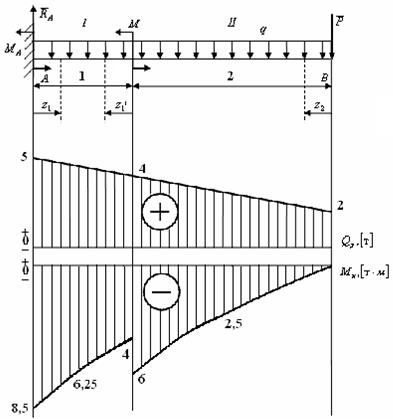
Рис. 5.4
Определение реакций в опорах:
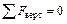 ;
;
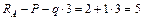 т.
т.
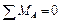 ;
;
 .
.
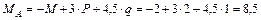 т·м.
т·м.
Проверка правильности определения реакций: в качестве проверочного уравнения моментов нельзя составлять уравнения относительно любой из опор конструкции:
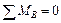 ;
;
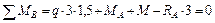 ;
;
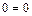 .
.
Первый способ решения задачи.
I: 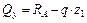 ;
; 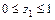
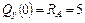 т;
т;
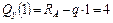 т;
т;
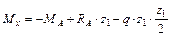 .
.
Любой силовой фактор, лежащий в конце участка, в уравнения сил и моментов не входит:
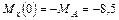 ;
;
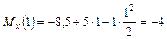 т·м;
т·м;
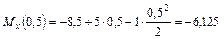 т·м.
т·м.
Проверка правильности решения эпюры изгибающих моментов: на участке действия кривой распределенной нагрузки выпуклость эпюры 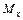 должна быть направлена навстречу распределенной нагрузке.
должна быть направлена навстречу распределенной нагрузке.
II. 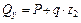 ,
, 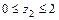
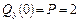 т;
т;
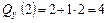 т;
т;
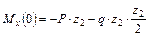 ;
;
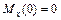 ;
;
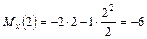 т·м;
т·м;
 т·м.
т·м.
Проверка правильности построения эпюр.
1. Любой скачок на эпюре 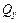 должен быть равен сосредоточенной силе, приложенной в этом сечении.
должен быть равен сосредоточенной силе, приложенной в этом сечении.
2. Любой скачок на эпюре 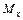 должен быть равен сосредоточенному моменту, приложенному в этом сечении.
должен быть равен сосредоточенному моменту, приложенному в этом сечении.
Второй способ решения задачи:
В консольной балке можно на каждом участке двигаться навстречу к жесткой заделке, при этом силовые факторы, расположенные в этой заделке, можно не рассчитывать, но на каждом участке двигаться по направлению к заделке. Для первого участка, при движении справа:
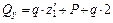 .
.
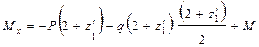 .
.
Дифференциальные зависимости при изгибе
Выделим из балки, находящейся под действием системы сил, бесконечно малый элемент двумя поперечными сечениями, отстоящими на расстоянии 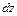 друг от друга (рис. 5.5). Слева действуют внутренние усилия
друг от друга (рис. 5.5). Слева действуют внутренние усилия 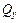 и
и  , справа
, справа 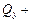
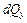 и
и 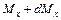 , а также на всем протяжении элемента распределенная нагрузка
, а также на всем протяжении элемента распределенная нагрузка 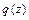 .
.

Рис. 5.5
Составим уравнение равновесия элемента в виде суммы проекций на вертикальную ось:
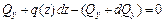 ;
;
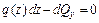 ;
;
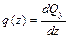 . (5.1)
. (5.1)
Первая производная от поперечной силы по абсциссе z равна интенсивности распределенной нагрузки, перпендикулярной оси балки.
Составим уравнение равновесия элемента dz в виде суммы моментов всех сил относительно точки O:
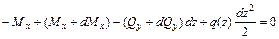 ;
;
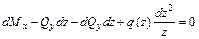 .
.
Отбрасываем бесконечно малые величины второго порядка:
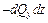 и
и  ;
;
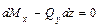 ;
;
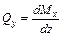 . (5.2)
. (5.2)
С учетом выражения (5.1), имеем
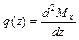 .
.
Вторая производная от изгибающего момента по абсциссе z равна интенсивности распределенной нагрузки перпендикулярной оси балки.
Особое значение имеет формула (5.2), так как она позволяет исследовать эпюру 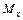 на экстремум.
на экстремум.
 2020-07-12
2020-07-12 91
91








