Свойства хорд, секущих и касательных

Углы треугольника

Во всяком треугольнике сумма улов равна 180° или π радиан.

 

Следствие 1. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Следствие 2. Сумма острых углов прямоугольного треугольника равна .

 

Пример. У треугольника один из внутренних углов равен 30°, а один из внешних 40°.

Найдите остальные внутренние углы треугольника.

 

Во всяком треугольнике:

1) против равных сторон лежат равные углы (и наоборот);

2) против большей стороны лежит больший угол (и наоборот).

 

Следствие. Пусть c – наибольшая

сторона; тогда:

а) если , то треугольник остроугольный;

б) если , то треугольник прямоугольный;

в) если  , то треугольник тупоугольный.

 

Теорема косинусов

Квадрат любой стороны треугольника АВС равен сумме квадратов двух других без удвоенного произведения этих сторон на косинус угла между ними.

 

Теорема синусов

Стороны треугольника АВС пропорциональны синусам противолежащих углов.

 

Пример. Длины сторон прямоугольного треугольника образуют арифметическую

прогрессию с разностью 1 см. Найдите длину гипотенузы.  

2. Равные и подобные треугольники.

Признаки равенства треугольников:

1. Если две стороны и угол, заключенный между ними, одного треугольника соответственно равны двум сторонам и углу, заключенному между ними, другого треугольника, то такие треугольники равны (первый признак равенства треугольников – по двум сторонам и углу между ними).

2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (второй признак равенства треугольников – по стороне и двум к ней прилежащим углам).

3. Если три стороны одного треугольника соответственно равны трем сторонам другого

треугольника, то такие треугольники равны (третий признак равенства треугольников

– по трем сторонам).

 

Пример. Докажите, что диагональ параллелограмма разбивает его на два равных треугольника.

 

Два треугольника и  называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

 

1. Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны (первуй признак подобия треугольников – по двум углам).

2. Если в двух треугольниках две пары сторон пропорциональны, а углы, заключенные между этими сторонами, равны, то треугольники подобны (второй признак подобия треугольников – по двум сторонам и углу между ними).

3. Если три стороны одного треугольника пропорциональны трем сторонам другого, то треугольники подобны (третий признак подобия треугольников – по трем сторонам).

 

Если два треугольника подобны, то любой линейный элемент (или сумма линейных элементов) одного треугольника относится к соответствующему линейному элементу (или сумме соответствующих линейных элементов) другого треугольника как соответственные стороны (обобщенная теорема подобия).

 

Пример.  1.Треугольник со сторонами 13, 14, 15 разделен на три равновеликие части

прямыми, перпендикулярными большей стороне. Найдите расстояния до этих прямых от ближайших к ним вершин треугольника, находящихся на большей стороне.

 

2. Основание треугольника равно 30 см, а боковые стороны 26 и 28 см. Висота разделена в отношении 2:3 (считая от вершины), и через точку деления проведена прямая, параллельная основанию. Найдите площадь полученной при этом трапеции.

 

3. Внутри прямого угла дана точка М, расстояние от которой до сторон угла равны 4 и 8. Прямая, проходящая через точку М, отсекает от прямого угла треугольник площадью 100. Найдите катеты треугольника.

 

3. Площадь треугольника.

Площадь треугольника равна половине произведения его стороны на проведенную к ней высоту.

Следствие 1. Площадь прямоугольного треугольника АВС () равна половине произведения его катетов.

Следствие 2. Если два треугольника имеют равные стороны, то отношение их площадей равно отношению соответственных высот, опущенных на эти стороны (или их продолжения).

Следствие 3. Если два треугольника имеют равные высоты, то отношение их площадей равно отношению соответственных оснований (сторон, на которые опущены эти высоты).

 

Площадь треугольника равна половине произведения двух любых его сторон на синус угла между ними.

Следствие. Если угол одного треугольника равен углу (или является дополнительным углом) другого треугольника, то отношение площадей этих треугольников равно отношению произведений сторон, содержащих эти углы.

 

Формула Герона. Площадь треугольника равна , где  - полупериметр.

 

Площадь треугольника равна 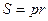, где r – радиус вписанной в треугольник

окружности, p – полупериметр.

 

Площадь треугольника равна , где R - радиус описанной около треугольника окружности.

 

Примеры. 1. Стороны треугольника равны 7, 24 и 25. Найдите его высоты.

2. В треугольнике АВС на стороне АС взята точка так, что .

Найдите площадь треугольника , если .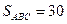

3. Точка М лежит внутри равностороннего треугольника на расстоянии  от двух его сторон и на расстоянии  от третьей стороны. Найдите длину стороны данного треугольника.

 

4. Медианы, высоты, биссектрисы.

Медианой треугольниканазывается отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

 

Во всяком треугольнике медианы пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.

 

В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

 

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине этой гипотенузы, а также радиусу окружности, описанной около этого треугольника.

 

Примеры. 1. Докажите, что три медианы треугольника делят треугольник на шесть

равновеликих треугольников.

2. Докажите, что длина медианы треугольника вычисляется через длины его

сторон по формуле: .

3. Докажите, что длина стороны треугольника по известным трем медианам вычисляется по формуле: .

 

Высотой треугольниканазывается перпендикуляр, проведенный из вершины треугольника на его противоположную сторону или ее продолжение.

 

Три высоты треугольника пересекаются в одной точке (ортоцентр).

 

Свойство серединного перпендикуляра. Если какая-нибудь точка лежит

на перпендикуляре, проведенном через середину отрезка, то она одинаково удалена от концов этого отрезка (и обратно).

 

Примеры. 1. Докажите, что высоты треугольника обратно пропорциональны сторонам.

2. В равнобедренном треугольнике боковая сторона равна b, а основание a. Найдите длину высоты, проведенной к боковой стороне.

3. Найдите углы треугольника, в котором высота и медиана, проведенные из одной вершины, делят угол при этой вершине на три равные части.

 

Биссектрисой треугольниканазывается отрезок биссектрисы угла треугольника от вершины до противоположной стороны треугольника.

 

Биссектриса есть геометрическое место точек, равноудаленных от сторон угла (свойство биссектрисы угла).

Во всяком треугольнике биссектрисы пересекаются в одной точке, являющейся центром вписанной в треугольник окружности.

 

Пример. Докажите, что биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.

 

Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника (свойство биссектрисы треугольника): .

 

Примеры. 1. Докажите, что большей стороне треугольника соответствует меньшая биссектриса.

2. Дан треугольник АВС такой, что АВ = 15 см, ВС = 12 см и АС = 18 см. В каком отношении центр вписанной в треугольник окружности делит биссектрису угла С?

3. Катеты прямоугольного треугольника равны 21 см и 28 см. Найдите длину биссектрисы прямого угла.

4. Найдите площадь прямоугольного треугольника, если известно, что биссектриса прямого угла разделила гипотенузу на отрезки 30 см и 40 см.

 

Занятие 2. Геометрия окружности.

 

План:

1. Свойства хорд, секущих и касательных.

2. Длина окружности. Площадь круга и его частей.

3. Касающиеся, пересекающиеся, непересекающиеся окружности.

 

Свойства хорд, секущих и касательных.

 

Окружностью называется множество точек плоскости, находящихся на одинаковом расстоянии от данной точки (центра окружности).

Кругом называется часть плоскости, ограниченная окружностью.

 

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром окружности.

 

Хорды, равноудаленные от центра окружности, равны.

Диаметр, перпендикулярный хорде, делит хорду и стягиваемые ею дуги пополам.

 

Касательной к окружности называется прямая, имеющая с окружностью одну общую точку.

Длины касательных, проведенных из одной точки вне круга к окружности, равны между собой.

Через точку, лежащую на окружности, можно провести лишь одну касательную к этой окружности.

Касательная перпендикулярна радиусу, проведенному в точку касания.

 

Если через точку M вне окружности провести две секущие, то произведения длин секущих на их внешние части будут равны (теорема о секущей):

 

 Если через точку M вне окружности провести секущую и касательную, то произведение длины секущей на ее внешнюю часть будет равно квадрату длины касательной (теорема о секущей и касательной): .

 

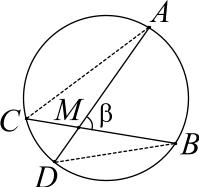
Если через точку M внутри окружности провести две пересекающиеся хорды AD и BC, то произведения отрезков этих хорд будут равны (теорема о хордах).

 

В одном круге или в равных кругах:

1) если дуги равны, то и стягивающие их хорды равны и одинаково удалены от центра;

2) если две дуги, меньшие полуокружности, не равны, то большая из них стягивается большей хордой и из обеих хорд большая расположена ближе к центру.

 

Центральный угол – угол, вершина которого лежит в центре окружности, а стороны являются радиусами. Величина центрального угла равна величине соответствующей дуги (выраженной в радианах или градусах).

Вписанный угол – угол, вершина которого лежит на окружности, а стороны являются хордами.

 

Величина вписанного угла равна половине дуги, заключенной внутри угла.

Следствие. Вписанный угол, опирающийся на диаметр, прямой.

Угол, составленный касательной и хордой, равен половине дуги, стягиваемой этой хордой.

 

Угол (составленный пересекающимися хордами) с вершиной внутри окружности равен полусумме соответствующих дуг: .

 

 

Примеры.

1. Через точку M, удаленную от центра окружности на расстояние b, проведена секущая MA так, что она делится окружностью пополам MB = BA. Определить длину секущей MA, если радиус окружности равен r.

2. Из внешней точки проведены к окружности секущая длиной 12 и касательная, длина которой составляет 2/3 внутреннего отрезка секущей. Найдите длину касательной.

3. Внутри круга радиуса 15 см взята точка М на расстоянии 13 см от центра. Через точку М проведена хорда длиной 18 см. Найдите длины отрезков, на которые точка М делит хорду.