Задача 1. (об использовании ресурсов).
Для изготовления двух видов продукции р1 и р2 используют четыре вида ресурсов s1, s2, s3, s4. запасы ресурсов, затрачиваемых на производство единицы продукции, приведены в таблице 1.
Таблица 1
| Вид ресурса | №запас ресурса | Число единиц ресурсов, затрачиваемых на изготовление единицы продукции | |
| р1 | р2 | ||
| s1 | 18 | 1 | 3 |
| s2 | 16 | 2 | 1 |
| s3 | 5 | - | 1 |
| s4 | 21 | 3 | - |
Прибыль, получаемая от единицы продукции р1 и р2 – соответственно 2 и 3 руб. Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.
Геометрический метод решения. Составим экономико-математическую модель задачи. Обозначим 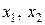 - число единиц продукции соответственно
- число единиц продукции соответственно 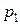 и
и 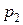 , запланированных к производству. Для их изготовления потребуется
, запланированных к производству. Для их изготовления потребуется 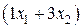 единиц ресурса
единиц ресурса  ,
, 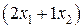 единиц ресурса s2,
единиц ресурса s2, 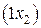 единиц ресурса
единиц ресурса 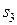 и
и 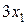 единиц ресурса
единиц ресурса  . Так как потребление ресурсов s1, s2, s3, s4 не должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выразится системой неравенств:
. Так как потребление ресурсов s1, s2, s3, s4 не должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выразится системой неравенств:
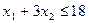 ,
,
 , (4)
, (4)
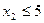 ,
,
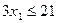 .
.
по смыслу задачи переменные
х1³0, х2³0 (5)
суммарная прибыль f составит 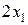 руб. от реализации продукции
руб. от реализации продукции 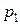 и
и  руб. - от реализации продукции р2, т.е.
руб. - от реализации продукции р2, т.е.
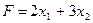 (6)
(6)
итак, экономико-математическая модель задачи: найти такой план выпуска продукции 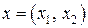 , удовлетворяющий системе (4) и условию (5), при котором функция (6) принимает максимальное значение:
, удовлетворяющий системе (4) и условию (5), при котором функция (6) принимает максимальное значение:
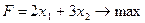
при ограничениях:

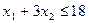 (i)
(i)
 (ii)
(ii)
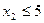 (iii)
(iii)
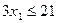 (iv)
(iv)
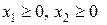 (v,vi)
(v,vi)
Изобразим многоугольник решений на рис. 1
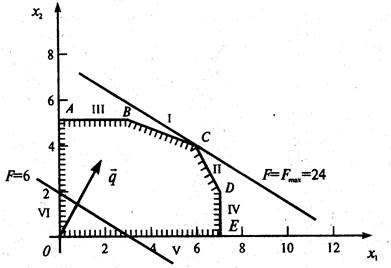
Рис. 1.
Очевидно, что при 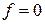 линия уровня
линия уровня 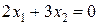 проходит через начало координат (строить ее не обязательно). Зададим, например,
проходит через начало координат (строить ее не обязательно). Зададим, например, 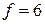 и построим линию уровня
и построим линию уровня 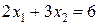 . Ее расположение указывает на направление возрастания линейной функции (вектор
. Ее расположение указывает на направление возрастания линейной функции (вектор 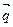 ). Так как рассматриваемая задача - на отыскание максимума, то оптимальное решение - в угловой точке с, находящейся на пересечении прямых i и ii, т.е. координаты точки с определяются решением системы уравнений
). Так как рассматриваемая задача - на отыскание максимума, то оптимальное решение - в угловой точке с, находящейся на пересечении прямых i и ii, т.е. координаты точки с определяются решением системы уравнений
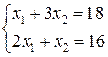
откуда 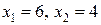 , т.е. С (6;4).
, т.е. С (6;4).
Максимум (максимальное значение) линейной функции равен 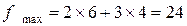 .
.
Итак, 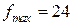 при оптимальном решении
при оптимальном решении 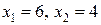 , т.е. максимальная прибыль в 24 руб. может быть достигнyта при производстве 6 единиц продукции р1 и 4 единиц продукции р2.
, т.е. максимальная прибыль в 24 руб. может быть достигнyта при производстве 6 единиц продукции р1 и 4 единиц продукции р2.
 2020-07-12
2020-07-12 176
176








