Пример решения задачи

Найти наибольшее и наименьшее значения функции

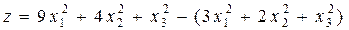
при условии, что х₁, х₂, х₃ удовлетворяют уравнению /

Решение. Уравнение связи определяет в пространстве сферу единичного радиуса с центром в начале координат рис. 3.

Так как сфера - замкнутое ограниченное множество, то согласно теореме Вейерштрасса функция достигает на ней своего наибольшего и наименьшего значений.

Рис. 3.

 

Необходимо найти условный глобальный экстремум. запишем уравнение связи в виде: .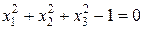

Составим функцию Лагранжа:

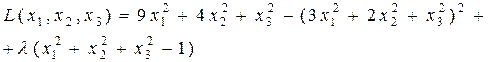
Найдем частные производные этой функции по х₁, х₂, х₃,.

,

,

,

.

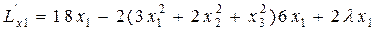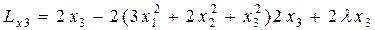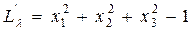Приравняв частные производные нулю, получим систему:

,

,

,

.

 

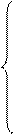
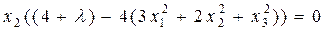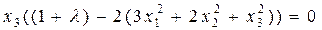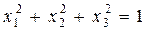Решая систему, получим стационарные точки, в которых найдем значения функции z:

1. ,

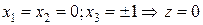2. ,

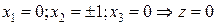3. ,

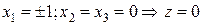4. ,

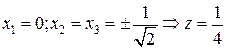5. ,

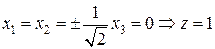6. .

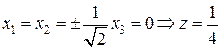Выберем из всех значений наибольшее и наименьшее: 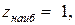 а
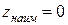. Легко видеть, в каких точках сферы доcтигаются эти значения.

ЗАДАЧА ВЫПУКЛОГО ПРОГРАММИРОВАНИЯ

Задача выпуклого программирования (ВП) состоит в отыскании такого решения системы ограничений (25), при котором целевая функция z достигает минимального значения, или вогнутая функция z достигает максимального значения.

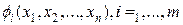                                      (25)