2020-07-12
108
при различных значениях υ f:
1 – 0,2; 2 – 0,55; 3 – 0,83; 4 – 0,78; 5 – 0,7
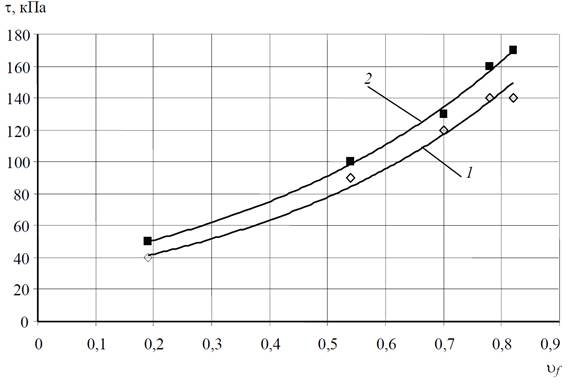
Рис. 2. Зависимость предельного напряжения сдвига
от объемной степени наполнения:
1 – через 5 мин; 2 – через 10 мин
Для определения вида аппроксимирующей функции τ = τ (υ f, t) воспользуемся методом сечений.
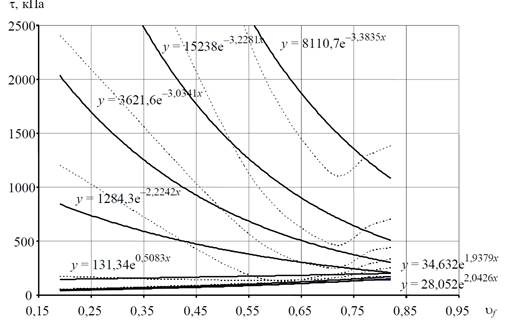
На рис. 3, а приводятся результаты аппроксимации функций τ = τ (υ f, t = const) функциями вида y =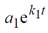 
, а на рис. 3, б – аппроксимация τ = τ (υ f = const, t) функциями вида y = 
.
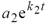На рис. 4 показана полиноминальная аппроксимация k 1 = k 1(υ f) и k 2 = k 2(t) при различных степенях полинома
а)
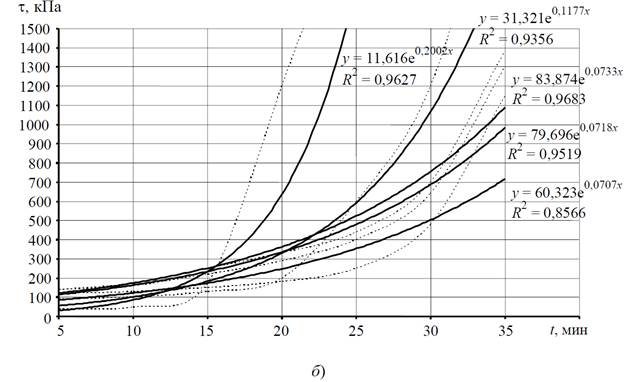
Рис. 3. Аппроксимации функций:
а – τ = τ (υ f, t = const); б – τ = τ (υ f = const, t)
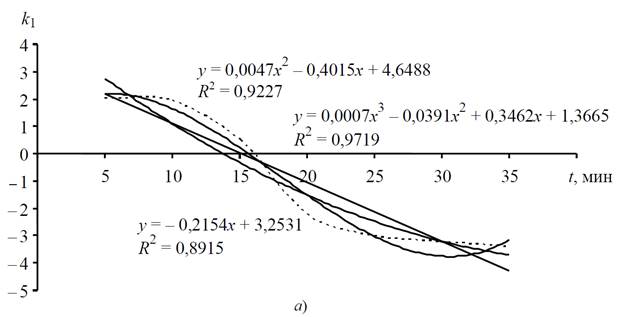
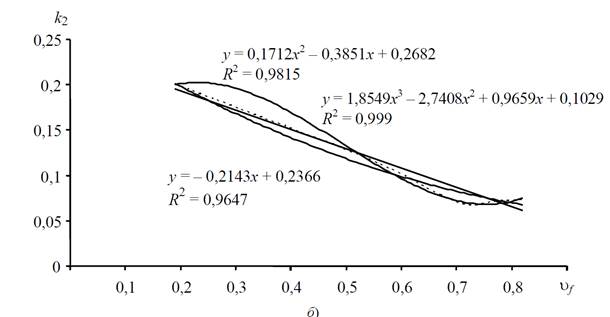
Рис. 4. Полиномиальная аппроксимация k 1 = k 1 ( υ f) (а) и k 2 = k 2(t) (б)
При различных степенях полинома
Из приведенных результатов с очевидностью следует возможность аппрокимации τ = τ (υ f, t) в виде
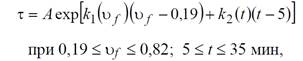
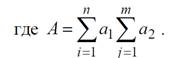
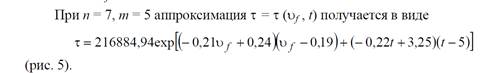
С применением полной диаграммы реологических свойств композиционных материалов можно проводить обоснованный выбор рецептурно-технологических параметров с учетом комплексного влияния указанных факторов на процессы структурообразования композиционных материалов.
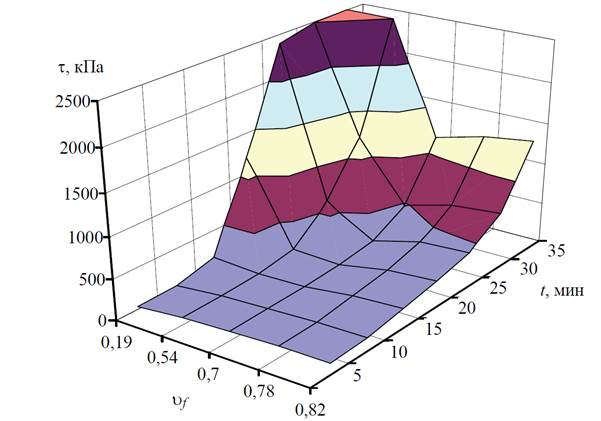
Рис. 5. Полная диаграмма реологических свойств
Радиационно-защитных эпоксидных композитов
Предложенный метод представления изменения реологических свойств (полная диаграмма) позволяет решить задачу оптимального синтеза композиционных материалов в случае действия множества структурообразующих факторов, то есть задачу многокритериального синтеза.
