Геометрический и физический смысл производной

Производнаяфункции f(x) – это f’(x), которая равна мгновенной скорости:

,

где 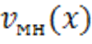 – мгновенная скорость в момент .

В этом заключается физический смысл производной.

 

 

Производная в точке х₀ – это также тангенс угла наклона касательной:

,

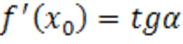где  – угол наклона касательной к кривой  в точке с абсциссой .

В этом заключается геометрический смысл производной.

 

Вопрос 4. Алгоритм нахождения производной

 

Определение производной не только с исчерпывающей полнотой характеризует понятие скорости изменения функции при изменении аргумента, но и даёт способ практического вычисления производной данной функции. Для этого необходимо выполнить следующие четыре действия (четыре шага), указанные в самом определении производной.

Для того чтобы найти  нужно:

1) Задать приращение  – это приращение аргумента.

2) Вычислить соответствующее приращение функции  или иначе: .

3) Найти разностное соотношение приращений , упростить его и сократить на .

4) Если отношение   при  стремится к какому-то числу, то это число есть – производная, обозначаем 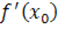, то есть находим производную функции f(x) или производную:

f '(x) = lim ∆y/∆x

∆х→0

 

 

Вопрос 5. Домашнее задание

 

Вопросы и задания (ответить письменно):

1 Что называется средней скоростью прямолинейного движения материальной точки?

1. Чему равна средняя скорость прямолинейного равномерного движения?

2. Как записать в виде отношения приращений мгновенную скоростью движущейся материальной точки, закон движения которой описывается функцией s = f(t)?

3. Чему равна мгновенная скорость равномерного движения?

4. Какая прямая называется секущей к кривой?

5. Какая прямая называется предельным положением секущей?

6. Какая прямая называется касательной к кривой?

7. Чему равен угловой коэффициент касательной к кривой, заданной уравнением y = f(x), в точке М₀(х₀; у₀)?