И приращение аргумента

Физический и геометрический смыслы

Производной

Вопросы темы:

Понятия: приращение функции и приращение аргумента.

Физический и геометрический смыслы отношения приращений.

Определение производной функции.

Алгоритм нахождения производной.

Домашнее задание.

Вопрос 1. Понятия: приращение функции

и приращение аргумента

 Рис.1

Рассмотрим некую произвольную, определенную и непрерывную на промежутке (a; b), функцию  (Рис.1), рассмотрим линию графика функции и дадим физическую интерпретацию:

Построим систему координат и кривую  (Рис.1), где

 независимая переменная или аргумент (время),

 – зависимая переменная или функция (расстояние),

 – закон (правило), по которому каждому значению  ставится в соответствие только одно значение .

 

Зафиксируем момент времени  (Рис.2). В этот момент времени можно вычислить расстояние по заданному закону , то есть имеем

точку А с координатами .

Эта точка А показывает, что в данный момент времени , расстояние составило – .

Дадим аргументу приращение , то есть прошло некоторое время  (приращение). Новый момент времени, который будет рассматриваться – это уже  (первоначальный момент времени плюс приращение времени (аргумента)).

 

 Рис.2

 

Построим секущую к графику функции 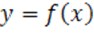 (Рис.2).

 – приращение аргумента – это разность между новым значением аргумента (времени) и старым ((х₀ + ∆х) – х₀).

Итак, в новый момент времени , имеем расстояние (от первоначального пункта) – .

Это расстояние можно вычислить по заданному закону, то есть если подставить в функцию новое значение независимой переменной (аргумента), то можно вычислить новое значение функции:

так получилась точка В (вторая точка, в которой секущая пересекает линию графика заданной функции) на графике функции имеем точку В с координатами

.

В результате получилась секущая , которая наклонена к оси  под углом .

 – секущая,  – ее угол наклона.

Этот угол, во – первых, в верхней полуплоскости и, во – вторых, с положительным направлением оси .

Рассмотрим треугольник  (Рис.3). Он прямоугольный. В этом треугольнике острый угол – это угол  – угол наклона секущей. Один из катетов (горизонтальный) – это приращение аргумента, а второй катет (вертикальный) – это разность между значением функции в новой точке и значением функции в старой точке (приращение функции).

 

 Рис.3

Приращение функции  =  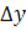и приращение аргумента  = ((х₀ + ∆х) – х₀) представлены на Рис.3.

Величину катета  обозначаем  – это приращение функции и вычисляется как разность значений функции в новый момент времени минус значение функции в старый момент времени

.

Вопрос 2. Физический и геометрический смыслы

отношения приращений ∆f/∆x

Рассмотрим отношение уже известных нам двух величин: ,

где  – приращение функции,

 – приращение аргумента (Рис.4).

1. Из физических соображений ясно, что отношение расстояния ко времени – это средняя скорость .

В этом заключается физический смысл отношения приращений .

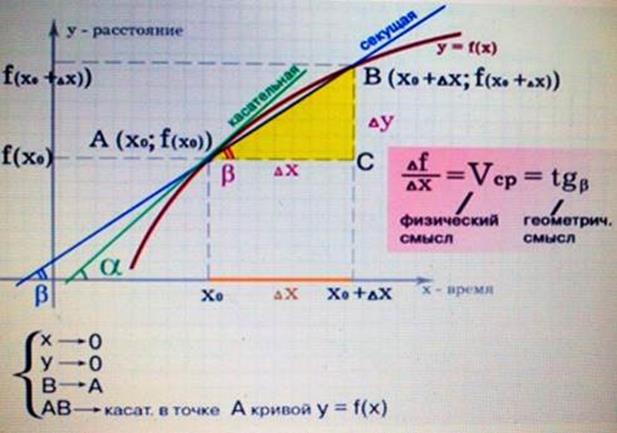 Рис.4

2. С другой стороны отношение катета 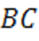 к катету  – это тангенс угла  – тангенс угла наклона секущей, то есть отношение приращений функции и аргумента  – это тангенс угла наклона секущей .

В этом заключается геометрический смысл отношения приращений .

 

Вопрос 3. Определение производной функции

Пусть приращение аргумента стремится к нулю: .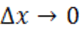

Понятно, что и приращение функции также будет стремиться к нулю: .

При этом, секущая, оставаясь неподвижной в точке А, будет менять угол наклона по отношению к оси Ох, а точка , означающая положение приращений аргумента (х) и функции (у) при их стремлении к нулю, будет стремиться к точке , а секущая  будет стремиться занять свое предельное положение - положение касательной в точке  к линии графика функции   (Рис.4).

 

Выразим в виде условных обозначений то, что имеем:

 

Зафиксируем эту касательную, при этом угол альфа  – это угол наклона этой касательной.

Это означает, что угол φ (фи) наклона секущей будет приближаться к углу ά (альфа) наклона касательной, а при этом тангенс угла φ будет стремиться а тангенсу угла ά:

tgφ → tgά     при .

Если зафиксировать точку , то отношение  зависит только от величины .

Если отношение  при  стремится к какому-то числу, то это число называется производной функции  в точке  и обозначается .

Определение:

Производной функции  в точке  называется число, к которому стремится разностное соотношение   при .

Определение производной с помощью предела:

Предел при 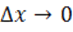 разностного отношения , если он существует, называется производной функции в точке  и обозначается .

Следовательно, соотношение приращений при 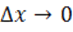 можно выразить с помощью предела:

lim ∆y/∆x = lim tgφ = tg ά = k,

∆х→0             ∆х→0

 

где k – это угловой коэффициент

касательной к линии графика функции.

Предел  lim ∆y/∆x в математике называют

∆х→0

производной функции или производной и обозначают f’(x).

 

С помощью этой формулы производной можно решить задачи по определению мгновенной скорости, силы переменного тока в проводнике и по определению углового коэффициента касательной к определенной точке кривой, а также задачи о скорости протекания химических реакций, нахождения линейной плотности неоднородного стержня, о величине теплоемкости тела при его нагревании, об угловой скорости вращающегося тела и другие.

 

Функция, имеющая производную в каждой точке интервала (a; b)  называется дифференцируемой в этом интервале;

Операция нахождения производной функции называется дифференцированием.

Если функция имеет производную в точке x=a, то говорят, что она дифференцируема в этой точке.

Если функция имеет производную в каждой точке данного промежутка, то говорят, что функция дифференцируема на этом промежутке.