Выражения и их преобразования

13.05.20

краткое повторение алгебры за 8 класс (основные понятия, формулы и определения). Вся информация, самое главное и всё, что нужно знать вкратце. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского) — М.: Просвещение, 2017

Выражения и их преобразования

■ 1. Выражения, составленные из чисел и переменных с помощью действий сложения, вычитания и умножения, называют целыми выражениями. При этом произведение одинаковых множителей может быть записано в виде степени. К целым выражениям относят и выражения, в которых, кроме действий сложения, вычитания и умножения, используется деление на число, отличное от нуля. Например, выражения а² + 3ab – 2b², (х – у)(2х + у²), m – n/3 целые.

Выражения, составленные из чисел и переменных, в которых, кроме действий сложения, вычитания и умножения, используется деление на выражение с переменными, называют дробными выражениями. Например, выражения х + 1/(x – 1), (a + 2)/b, 5m: n дробные.

Целые и дробные выражения называют рациональными выражениями.

Целое выражение имеет смысл при любых значениях входящих в него переменных. Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение a + 1/(a – 2) не имеет смысла при а = 2, выражение 3/(x – y) не имеет смысла при х = у.

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных

■ 2. Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

Два выражения, принимающие равные значения при всех допустимых для них значениях переменных, называют тождественно равными, а замену одного выражения другим, тождественно равным ему, — тождественным преобразованием выражения.

■ 3. Одночленами называют произведения чисел, переменных и их степеней, а также сами числа, переменные и их степени. Например, 8а³b, –1,5xy²z⁸, 12, с, m¹⁰ — одночлены.

Степенью одночлена называется сумма показателей степеней всех входящих в него переменных. Например, степень одночлена 9а⁷b равна 8.

■ 4. Многочленом называется сумма одночленов. Например, у⁴ – 8у³ + 2у – 3, 4а⁴b + 11а²b² – ab + 3b – 1 — многочлены. Одночлены считают многочленами, состоящими из одного члена.

Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 18а⁶ – 7а⁴b³ + 1 равна степени одночлена –7а⁴b³, т. е. равна 7. Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.

■ 5. При сложении многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например, (5х² – 3ху) + (4ху – 2х² + 1) = 5х² – 3ху + 4ху – 2х² + 1 = = 3x² + ху + 1.

При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например, (8а² – 3ab) – (7а² – 4ab + 5) = 8а² – 3ab –7а² + 4аb – 5 = а² + ab – 5.

Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например, 2x²(3x³– ху + 5у²) = 6х⁵ – 2х³у + 10х²у².

Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например, (2а – 3)(3а² + а – 4) = 6а³ + 2а² – 8а – 9а² – За + 12 = 6а³ – 7а² – 11а + 12.

Любое целое выражение можно представить в виде многочлена.

■ 6. Формулы сокращённого умножения.

а) (а + b)² = а² + 2ab + b².

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения.

б) (а – b)² = а² – 2ab + b².

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения.

в) (а + b)³ = а³ + 3а²b + 3ab² + b³.

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго плюс куб второго выражения.

г) (а – b)³ = а³ – 3а²b + 3ab² – b³.

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго минус куб второго выражения.

д) (а – b)(а + b) = а² – b².

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

е) а³ + b³ = (а + b)(а² – ab + b²).

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

ж) а³ – b³ = (а – b)(а² + ab + b²).

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

■ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.

Для разложения многочленов на множители применяют вынесение множителя за скобки, группировку, используют формулы сокращённого умножения. Например, многочлен 8а³ – 6аb можно разложить на множители, вынося 2а за скобки: 8а³ – 6аb = 2а (4а² – 3b); многочлен 2ab + 10b – За – 15 можно разложить на множители, используя группировку:

2ab + 10b – 3а – 15 = (2аb + 10b) – (За + 15) = 2b(а + 5) – 3(а + 5) = (а + 5)(2b – 3);

многочлен 9а² – 25b⁴ можно разложить на множители, используя формулу разности квадратов:

9а² – 25b⁴ = (3а)² – (5b²)² = (3а – 5b²)(3а + 5b²).

■ 8. Рациональной дробью называется выражение вида a/b, где а и b — многочлены.

При любых значениях а, b и с, где b ≠ 0 и с ≠ 0, верно равенство a/b = ac/bc. Это равенство сохраняет силу и в том случае, когда под буквами а, b и с понимают многочлены, причём b и c — ненулевые многочлены. Свойство дроби, выраженное тождеством a/b = ac/bc называют основным свойством дроби. Основное свойство дроби используется при сокращении дробей. Например:

Если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному:

■ 9. Действия над рациональными дробями выполняются аналогично действиям над обыкновенными дробями.

а) Если с ≠ 0, то

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же. Например:

Чтобы выполнить вычитание дробей с одинаковыми знаменателями, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же. Например:

б) Чтобы выполнить сложение или вычитание дробей с разными знаменателями, нужно привести их к общему знаменателю и затем применить правило сложения или вычитания дробей с одинаковыми знаменателями. Например: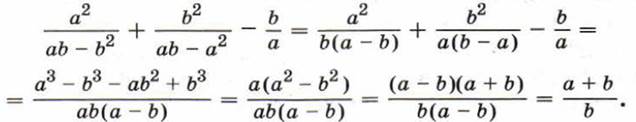

в) Если b ≠ 0 и d ≠ 0, то (a/b)*(c/d) = ac/bd.

Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе — знаменателем дроби. Например:

г) Если b ≠ 0, с ≠ 0 и d ≠ 0, то

Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй. Например:

Любое рациональное выражение можно представить в виде рациональной дроби.

■ 10. Степень с целым показателем.

Если n — натуральное число, большее 1, и а — любое число, то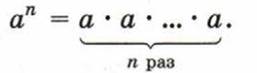

Если n = 1 и а — любое число, то a¹ = a.
Если n = 0 и а — число, отличное от нуля, то а⁰ = 1.
Если n — целое отрицательное число и а — отличное от нуля число, то

■ 11. Свойства степени с целым показателем.

а) а^mаⁿ = а^m+n, где а ≠ 0, m и n — целые числа.

При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают.

б) а^m: аⁿ = а^m–n, где а ≠ 0, m и n — целые числа.

При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

в) (а^m)ⁿ = а^mn, где а 0, m и n — целые числа.

При возведении степени в степень основание оставляют прежним, а показатели степеней перемножают.

г) (ab)ⁿ = аⁿbⁿ, где а ≠ 0 и b ≠ 0, n — целое число.

При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.

д) (a/b)ⁿ = aⁿ/bⁿ, где а ≠ 0 и b ≠ 0, n — целое число.

При возведении в степень дроби возводят в эту степень числитель и знаменатель и первый результат записывают в числителе, а второй — в знаменателе дроби.

■ 12. Квадратным корнем из числа а называется число, квадрат которого равен а.

Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а. Арифметический квадратный корень из а обозначают √a. Выражение, стоящее под знаком корня, называют подкоренным выражением. Выражение √а имеет смысл для всех а ≥ 0 и не имеет смысла при а < 0.