По теме «Решения уравнений графическим способом»

Урок №16 от 18.05.2020

 

Рекомендации: для лучшего понимания темы просмотрите видео, конспект, дополнительные материалы, а также выполните задания на сайте https://resh.edu.ru

Решение уравнений графическим способом

Ø https://resh.edu.ru/subject/lesson/1548/start/

Графический способ решения линейных уравнений

Ø https://resh.edu.ru/subject/lesson/1212/

 

Рекомендации: для лучшего понимания темы просмотрите видео на сайте www.youtube.com:

Ø Решение уравнений графическим способом

https://www.youtube.com/watch?v=O8nE21JLpxw

 

· Ещё раз внимательно ознакомьтесь с решением следующих заданий по теме «Примеры решения уравнений графическим способом».

 

Задания:

1) Решите уравнение  графическим способом.

2) Решите уравнение 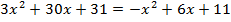 графическим способом.

3) Решите уравнение 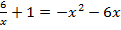 графическим способом.

4) Решите уравнение 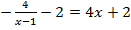 графическим способом.

 

Решение:

1) Решите уравнение  графическим способом.

Решение: представим данное уравнение в виде двух функций, приравняв  отдельно к левой и правой части данного уравнения: 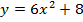 и ;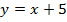

построим графики получившихся данных функци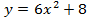й  и :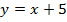

1) графиком функции 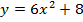 является парабола,

найдём координаты вершины параболы:

, ,

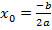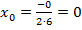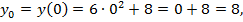
точка 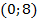 - вершина параболы

составим таблицу значения:

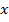
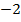
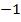
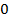
				1	2
	32	14		14	32

,

,

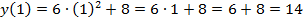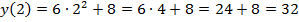2) графиком функции 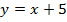 является прямая, поэтому достаточно координат двух точек для построения, составим таблицу значения:

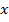
	0	1
	5	6

,

,

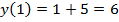Построим графики данных функций в одной координатной плоскости:

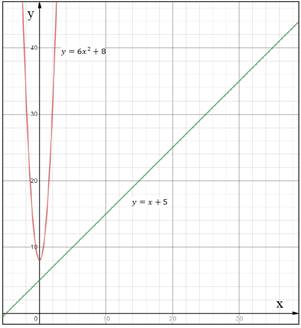
По чертежу четко видно, что графики данных функций не пересекаются, поэтому уравнение  не имеет корней.

Ответ: корней нет

 

2) Решите уравнение 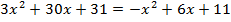 графическим способом.

Решение: представим данное уравнение в виде двух функций, приравняв  отдельно к левой и правой части данного уравнения:  и  ;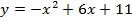

построим графики получившихся данных функци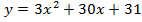й  и
:

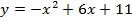1) графиком функции 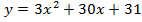 является парабола,

найдём координаты вершины параболы:

, ,

 

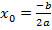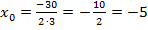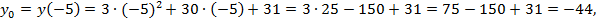
точка 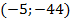 - вершина параболы

составим таблицу значения:

,

,

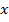
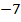
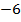
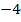
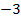
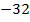
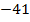
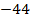
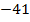
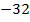
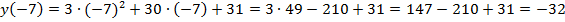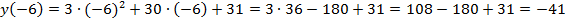2) графиком функции 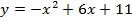 является парабола,

найдём координаты вершины параболы:

, ,

 

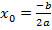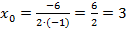точка 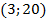 - вершина параболы

составим таблицу значения:

,

,

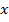
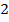
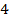
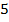
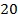
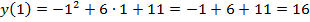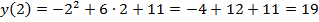Построим графики данных функций в одной координатной плоскости:

Графики данных функций пересеклись в двух точках:

в точке с координатами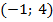

и в точке с координатами

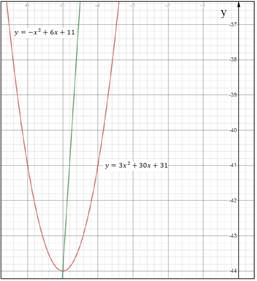
то есть уравнение имеет два корня: 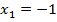 и .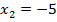

Однако по чертежу сложно точно определить координаты точек (в частности в этом случае пришлось изменять величину единичного отрезка несколько раз), поэтому необходимо сделать проверку.

Проверка: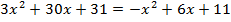

,

, ,

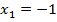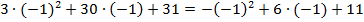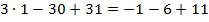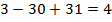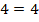, , верно;

,

, ,

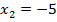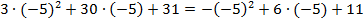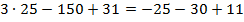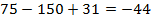, , верно.

Ответ: .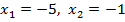

 

3) Решите уравнение 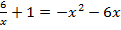 графическим способом.

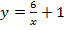Решение: представим данное уравнение в виде двух функций, приравняв  отдельно к левой и правой части данного уравнения:  и ;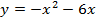

построим графики получившихся данных функци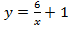й  и :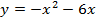

1) графиком функции 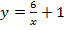 является гипербола, которую можно построить путем сдвига:

1) построим таблицу значений для функции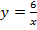

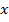
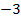
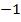
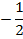
					1	3

,

,

,

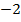
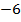
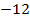
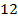
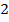
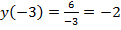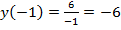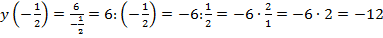2) сдвиг по оси ординат на 1 единицу вверх

2) графиком функции 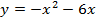 является парабола,

найдём координаты вершины параболы:

, ,

 

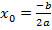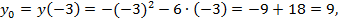
точка 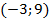 - вершина параболы

составим таблицу значения:

,

,

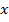
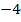
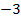
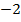
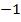
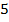
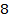
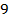
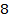
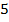
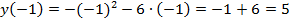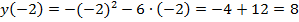Построим графики данных функций в одной координатной плоскости:

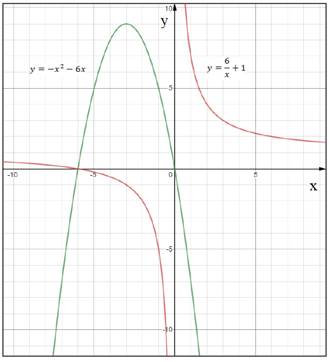
Графики данных функций пересеклись в одной точке:

в точке с координатами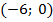

то есть уравнение имеет два корня: .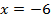

Однако по чертежу сложно точно определить координаты точек, поэтому необходимо сделать проверку.

Проверка: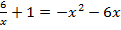

,

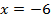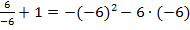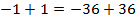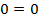, , , верно.

Ответ: .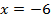

 

4) Решите уравнение 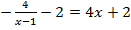 графическим способом.

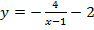Решение: представим данное уравнение в виде двух функций, приравняв  отдельно к левой и правой части данного уравнения:  и ;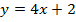

построим графики получившихся данных функци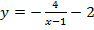й  и :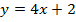

1) графиком функции 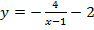 является гипербола, которую можно построить путем сдвига:

1) построим таблицу значений для функции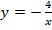

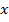
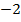
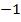
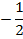
					1	2

,

,

,

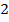
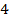
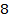
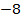
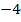
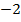
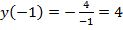2) сдвиг по оси ординат на 2 единицы вниз и по оси абсцисс на 1 единицу вправо

2) графиком функции 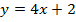 является прямая, поэтому достаточно координат двух точек для построения, составим таблицу значения:

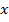
	0	1
	2	6

,

,

 

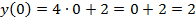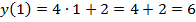Построим графики данных функций в одной координатной плоскости:

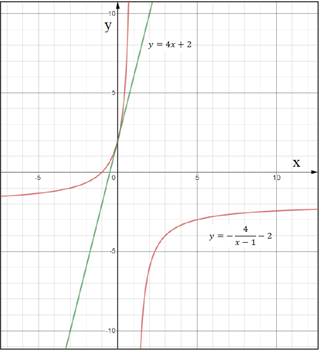
Графики данных функций пересеклись в одной точке:

в точке с координатами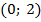

то есть уравнение имеет два корня: .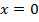

Однако по чертежу сложно точно определить координаты точек, поэтому необходимо сделать проверку.

Проверка: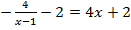

,

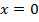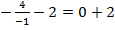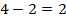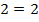, , ,  верно.

Ответ: .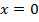

 

· Выполните домашнее задание.

Домашнее задание:

1) С. 222-223 §10 п. 10.4 читать

2) Выполните карточку

 

Карточка

Решить уравнение графическим способом:

1) 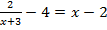;   2) .

 

 

· Решение домашнего задания оформите в тетради.

 

· Сфотографируйте в разборчивом виде.

 

· Передайте мне до 20.05.2020 через эл.дненик, Whatsapp, или VK.

 

Критерии оценивания карточки из домашнего задания:

Решение каждого из уравнений оценивается следующим образом:

Верное преобразование одного уравнения в функцию – 1 балл.

Верное построение одного графика функции – 1 балл.

Верный ответ – 1 балл.

Баллы суммируются.

Максимальное количество баллов за 1 уравнение – 5 баллов.

Максимальное количество баллов за всю работу – 10 баллов.

 

Перевод суммы баллов за все примеры в оценку:

ü 10 баллов – оценка «5»

ü 8 – 9 баллов – оценка «4»

ü 5 – 7 баллов – оценка «3»

ü менее 5 баллов – оценка «2»