Таким образом, оказалось, что свет обнаруживает корпускулярноволновой дуализм: обладает и
свойствами волн, и свойствами частиц. Эти свойства с макроскопической точки зрения противоречат друг другу: волна непрерывна, частица - дискретна; волна - безгранична, частица - ограничена в пространстве. Как совместить эти противоречащие друг другу свойства? Эта задача была решена. Установить связь между волновой и корпускулярной картинами можно с помощью статистического подхода.
Запишем уравнение электромагнитной волны (Е - напряжённость электрического поля волны; Е0 - амплитуда):
E = E 0 cos(w • t - kr). (21.4)
Тогда вероятность dp того, что фотон будет обнаружен в малом объёме dV вблизи точки с радиус-вектором Г (или координатами x,y,z), пропорциональна E0 - квадрату амплитуды волны и объёму dV:
dp = a • E0 • dV, (21.5)
Здесь a - некоторый коэффициент пропорциональности. Таким образом, распределение фотонов носит статистический характер. Квадрат амплитуды волны определяет вероятность попадания фотона в данную точку.
3. Гипотеза де Бройля
В 1923 г. Луи де Бройль выдвинул гипотезу, что корпускулярно-волновой дуализм универсален, то есть частицы обладают волновыми свойствами. Существует симметрия: если свет (волна) обладает корпускулярными свойствами, то почему бы частицам не проявлять свойства волновые? Природа едина.
Короче, всем частицам (фотонам, протонам, электронам, нейтронам, атомам, молекулам,...) приписываем
У корпускулярные свойства (энергию E и импульс p) и
У волновые свойства (длину волны l и частоту n).
При этом длина волны связана с импульсом для любой частицы так же, как и для фотона (см. лекцию № 20):
h
l = h. (21.6)
p
Это - длина волны де Бройля.
Для любой частицы справедливы соотношения:
| Корпускулярные свойства | Волновые свойства |
| E = hn | E П = h |
| h p = — l | l = h- p |
Движущейся частице с импульсом p и энергией E сопоставлена волна: у = Уо cos(w • t - к • r),
| E w = -. (21.7) h |
,, h.
E = hn =--- 2лп = h •w ^
2 л
h
Здесь h =------------ постоянная Планка с чертой. Волновой вектор равен:
2л
2л _ 2л • p _ p fД’ h h I p 0
у = y0cos —• t -±-
| у (х) = У о cosf E • t - p • x V h h0 |
| (21.8) |
Для волны, бегущей вдоль оси OX (частицы, движущейся вдоль оси OX):
(Смысл функции у пока прояснять не будем.)
Подтверждение гипотезы де Бройля было получено экспериментально (1927 год) при наблюдении дифракции электронов:
1) Опыты Дэвиссона и Джермера. Отражение электронов от кристалла никеля подчиняется формуле Брэгга-Вульфа (см. лекцию № 18):
2d • sin 0 = ±ml, m = 1, 2,.... (21.9)
2) В опытах Дж. Томсона исследовалась дифракция электронов на тонкой металлической поликристаллической фольге (рис.21.4). На фотопластинке появлялась дифракционная картина в виде концентрических колец, опять же в соответствии с формулой Брэгга-Вульфа. Электроны, ускоренные в электрическом поле разностью потенциалов U, имеют энергию
2 2
eU = mu 2.
2 2me
Тогда длина волны де Бройля
hh
l = -=, =. (21.10)
p yl2meeU
Совпадение длин волн, предсказанных де Бройлем по (21.10) и полученных из эксперимента по (21.9), совпали с точностью до 1%. Волновые свойства электрона обнаружились и в других экспериментах. Более того, удалось 68
наблюдать дифракцию нейтронов на кристаллах (1936 год), а также атомов (гелий) и молекул (водород). Есть эксперименты по дифракции больших молекул на специально созданной дифракционной решётке. Замечательно, что волновые свойства присущи каждой частице: дифракционная картина наблюдается и в случае очень слабых пучков, когда частицы летят поодиночке.
4. Микрочастица в двухщелевом интерферометре
Иллюстрацией двойственности свойств микрочастиц является опыт с двухщелевым интерферометром. Диафрагма с двумя щелями обстреливается
| * $2 Открыта 1 -я щель |
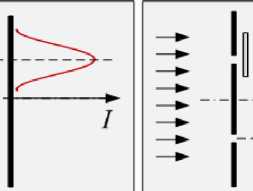
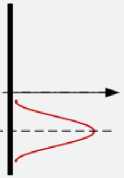
| Открыта 2-я щель |
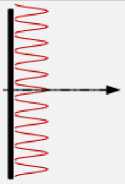
| Открыты обе щели; результаты эксперимента |
| потоком микрочастиц (электронов), которые затем попадают на экран (рис.21.4). Если открыта одна щель, напротив неё на экране получается полоса. Открывая вторую щель, ожидаем получить на экране две полосы, то есть простое сложение картинок при одной и второй открытой щелях, как это было бы в макромире при обстреле диафрагмы с |
| Рис.21.4 |
| Открыты обе щели; ожидаемая картина |
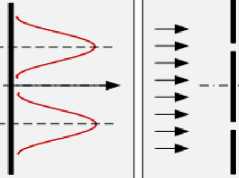

| Рис.21.5 |
| Электроны (и любые |
щелями обычными пулями. Но в опытах с микрочастицами на экране появляется типичная интерференционная картина, характерная для световых волн в аналогичном опыте Юнга. Электроны интерферируют при прохождении через две щели.
Пули дискретны, неделимы: каждая проходит через какую-то одну из двух щелей; никакой интерференции нет. Электрон, как и пуля, дискретен: он не может разделиться и пройти одновременно через обе щели.
Проделаем тот же эксперимент с волнами (рис.21.5): волна проходит через обе щели, она непрерывна. Для волн нет дискретности; есть интерференция.
микрочастицы) дискретны, как пули, но испытывают интерференцию, как волны.
Могло создаться впечатление, что микрочастицы интерферируют, потому что взаимодействуют друг с другом. Но даже для очень слабых пучков, когда микрочастицы летят поодиночке, интерференционная картина сохранялась, только нужно было подождать достаточно долго, чтобы картина достаточно проявилась. Электроны как будто «знают», что открыты обе щели, и попадают в нужные места экрана: туда, где должны быть интерференционные максимумы. Электрон интерферирует сам с собой? На движение одиночного, дискретного и неделимого электрона оказывают влияние обе щели. Как это понять? Приходится принять, что микрочастица обладает принципиально иными свойствами, чем макрочастица. У микрочастиц нет траектории.
Электрон не может «разделиться» на половинки и пролететь сразу через обе щели. Всё-таки хотелось бы знать, через какую щель пролетел электрон. «Подсмотрим» за электроном, поставив сразу за каждой из щелей источник света. Электрон, прошедший через данную щель, будет рассеивать свет, и мы это «увидим», то есть будем точно знать, через какую из щелей прошёл электрон; а если он, разделившись, пройдёт сразу через две щели, вспышки у каждой из щелей произойдут одновременно. В этом эксперименте получили, что электрон проходит только либо через одну щель, либо только через вторую. Но при этом никакой интерференции нет. Выключаем источники света, и картинка интерференции появляется снова.
Если не знаем координату (неизвестно, через какую щель пролетела микрочастица), то интерференция есть; тогда знаем длину волны де Бройля, знаем импульс частицы:
h
p = .
l
Лде Бройля
Если будем фиксировать, через какую щель прошёл электрон (включили лампочку), то не получим интерференции. Если знаем координату электрона (пролетел через данную щель), то не знаем длину волны, не знаем импульс.
5. Соотношение неопределённостей
Из корпускулярно-волнового дуализма микрочастиц вытекает, что нельзя одновременно точно знать её координату и импульс. Нельзя сказать: длина волны в данной точке; волна - протяжённый в пространстве объект. Если точно знаем импульс частицы, то знаем длину волны де Бройля (21.6):
l --h-,
Р можем записать волновое уравнение (21.8), но совершенно не знаем, где находится наша частица: гармоническая волна в пространстве бесконечна.
В 1927 году подобные соображения были сформулированы Гейзенбергом в виде принципа неопределённостей. Произведение неопределённостей координаты и соответствующей проекции импульса частицы не меньше h:
Apx -A x > h. (21.11)
Аналогично, для осей OY и OZ:
Apy -Ay > h;
Apz - Az > h.
Существуют пары физических величин, которые, подобно импульсу и координате, нельзя измерять одновременно точно. Такие величины называются сопряжёнными динамическими переменными. Это время и энергия; момент импульса L и угловая координата ф. Запишем принцип неопределённостей для таких сопряжённых величин:
DE-Dt > h; (21.11а)
DL-j > h. (21.11б)
Здесь DE - неопределённость энергии, Dt - неопределённость момента измерения энергии.
Принцип неопределённостей Гейзенберга не связан с несовершенством приборов или методов измерения; является спецификой микрочастиц - проявлением корпускулярно-волнового дуализма.
6. Волновая функция, её вероятностная интерпретация и свойства
Квантовая механика была создана в начале 20-го века. В ней учитываются волновые свойства микрочастиц. Авторы квантовой механики: Планк, Г ейзенберг, Шрёдингер, Борн. Состояние микрообъекта в квантовой механике описывается волновой функцией (пси-функция) Y(x, y, z, t). В общем случае это - функция координат и времени; а значения функции - комплексные. Смысл функции: квадрат модуля волновой функции определяет вероятность нахождения частицы в данной точке, то есть вероятность dp обнаружить частицу в объёме dV вблизи заданной точки с координатами x, y, z в момент времени t равна
dp = |Y(x, y, z, t)2 - dV; (21.12)
dp = Y-Y* - dV, (21.12а)
где Y* - комплексно сопряжённая функция.
Плотность вероятности обнаружения частицы в данной точке равна квадрату модуля волновой функции:
| (21.13) |
dV
Свойства волновой функции:
1) Однозначна, конечна, непрерывна, дифференцируема.
2) Вероятность pV найти частицу в конечном объёме V равна (из (21.12)):
PV = J|Y|2 - dV. (21.14)
V
3) Вероятность найти частицу хотя бы где-нибудь (неважно, в какой
точке пространства) - достоверное событие, если частица существует; поэтому сумма всех вероятностей по всему пространству есть единица:
+ ¥
| (21.15) |
Это - условие нормировки. Уточнение: интеграл в (21.15) берётся по всей области определения функции.
4) Волновую функцию можно домножить на любое комплексное число С, и полученная функция будет описывать то же самое состояние: Y и N • Y описывают одинаковые состояния частицы.
5) Если частица может находиться в состоянии, описываемом функциями Y, или Y, ■■■, или Ч(у, то возможно состояние частицы, описываемое любой линейной комбинацией этих функций:
Y= EQ -Y, (21.16)
i =1
где Ci - комплексные числа. Это свойство называется принципом суперпозиции. Именно оно легло в основу экспериментов по квантовой телепортации.
6) Зная волновую функцию состояния, можно найти среднее значение любой физической величины В:
B = JY«B •Y* • dV = f|Y|2 • B • dV. (21.17)
по области -да
определения функции
Описание состояния частицы с помощью волновой функции не позволяет найти ни координаты частицы, ни её траекторию. Однако утверждается, что волновая функция даёт исчерпывающее описание поведения микрочастицы. Волновая функция не даёт информации о том, чего нет: у микрочастиц нет траектории, нет точных значений координат в любой момент времени.
7. Уравнение Шрёдингера
7.1. Нестационарное (временн о е) уравнение Шрёдингера
Уравнение Шрёдингера - основное уравнение квантовой механики. Оно получено в 1926 году. Решением уравнения Шрёдингера получают волновую функцию состояния Y(x, y, z, t). Уравнение не доказывается теоретически и не может быть выведено из других соотношений. Можно сказать, что уравнение Шрёдингера - постулат квантовой механики, аналогично законам Ньютона в классической механике. Законы Ньютона - обобщение большого количества опытных данных. С уравнением Шрёдингера немножко сложнее: справедливость его доказывается тем, что следствия из него согласуются с опытом.
Временн о е уравнение Шрёдингера:
h 2 6Y
• \Y ■ U -Y = ih • —. (21.18)
2m dt
Здесь Y(x, y, z, t) - функция координат и времени (поэтому уравнение - 2
временн о е); i - мнимая единица (i = -1); \ - оператор Лапласа:
д2 д2 д2 d2Y д2— д2—
\ \ ■ „ ■ „; А— = ——+ —— + ——; (21.19)
дх2 ду2 dz2 дх2 ду2 dz2
U = U(х, у, z, t) - потенциальная функция частицы. Если U = U(х, у, z) зависит только от координат, но не зависит от времени, то это - потенциальная энергия частицы.
7.2. Стационарное уравнение Шрёдингера
Оказывается, что если U = U(х, у, z) не зависит от времени, то полную волновую функцию —(х, у, z, t) можно представить в виде произведения координатной y = f (х, у, z) и временн о й частей e l<wt = f (t), зависящих только от координат или только от времени соответственно:
—(х, у, z, t) = у (х, у, z) • e~lwt; (21.20)
А—(х, у, z, t) = e~lwt ■ Ау(х,у, z), (21.21)
поскольку временн а я часть не зависит от координат, а в оператор Лапласа входят только частные производные по координатам. Далее,
-— = ~У(х,у,z)• e^l(wW)= у(х,у z)• — (e^l(wW)= у • (- w) e^l(wW. (21.22)
д д^ дГ
Подставляем (21.21) и (21.22) во временн о е уравнение Шрёдингера (21.18) и сокращаем на e~l(wt:
2
- ±_ • e ~lw't •Ay + U • e ~lwt у = ih у • (- iw) • e ~lwt •
2m
h 2
- — • Ау + U у = lh у •(- lw).
2
Полная энергия частицы по (21.7) E = h w; l = -1; тогда
h 2
------ А у + U у = E у;
2 m
| (21.23) |
Это - стационарное уравнение Шрёдингера.
7.3. Собственные функции, собственные значения
Решение уравнения Шрёдингера существует не для любых значений энергии Е. Значения энергии, при которых решение существует, называются собственными значениями. Соответствующие им волновые функции у тоже называются собственными функциями.
Совокупность собственных значений энергии - спектр (энергетический спектр). Спектр энергии может быть дискретным (набор конкретных значений) или непрерывным, сплошным. Если спектр дискретный, собственные значения можно пронумеровать:
E 1, E 2, E3,-Ei,•
Этим значениям соответствуют собственные функции:
E 1 ® У1,
Е2 ® У2,
Ei ® Wi,
• • •.
Возможен случай, когда одному и тому же собственному значению энергии соответствует несколько волновых функций; например, три:
En ® Wni; Wn2; Wn3-
Тогда соответствующий уровень энергии называется вырожденным, причём кратность вырождения равна числу волновых функций. В приведённом примере уровень Ап трижды вырожден.
Замечание: квантование энергии при решении уравнения Шрёдингера получается естественно, без привлечения каких-либо дополнительных соображений.
8. Применение уравнения Шрёдингера
8.1. Одномерное движение свободной частицы
Пусть частица движется в постоянном потенциальном поле; потенциальная энергия частицы меньше её полной энергии: U = const < E. Рассматривается одномерное движение вдоль оси OX, тогда волновая функция зависит только от координаты x (y = y(x)), и стационарное уравнение Шрёдингера (21.23) примет вид: d-W + 2 ^ (E - U)- y = 0. Обозначим к 2 = "^ (E - U)> 0. Тогда
dx2 h 2 h 2
d 2.,,
—У + к 2 - y = 0 «> y " + к 2 - y = 0.
dt 2
Это обыкновенное дифференциальное однородное уравнение второго порядка.Егорешение - гармоническая функция: y(x)= A - cos(k - x). Здесь 7___ 2 m I 1 ' T t\ 1____ ^ft 7 7. _____ _ rZ____ _____
к = ^ -2- (E - U) - волновое число; к = -|. Можно записать общее решение,
помня, что волновая функция y - комплексная:
y(x)= A - /** + B - e-'к ' x.
Полная функция:
Y(x, t) = y(x)- e ~iw-t = (a - еьк - x + B - e ~ьк - x)- e ~iw-t;
Y(x, t)= A-e ~i -( w-t - 'x) + B-e-i-(w-t + k -x).
Получили суперпозицию двух волн: первое слагаемое представляет собой волну, бегущую в положительном направлении оси OX, второе - в отрицательном.
Действительная часть пси-функции - это суперпозиция двух косинусов (по формуле Эйлера elj = cos j + i sin j):
Re Y(x, t) = A ■ cos(w ■ t - k ■ x) + B ■ cos(w ■ t + k ■ x).
8.2. Частица в одномерной потенциальной яме с бесконечно высокими стенками
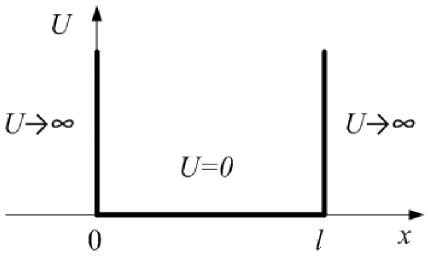
Рассмотрим частицу в одномерной потенциальной яме шириной l с бесконечно высокими стенками (рис.21.6). Потенциальная энергия частицы U обращается в бесконечность при x < 0 и x > l и равна нулю при 0 < x < l Найдём возможные значения энергии частицы в таком потенциальном поле и соответствующие волновые функции.
За пределы потенциальной ямы частица выйти не может, так как там U ®¥. Следовательно, волновая функция равна нулю при x < 0 и x > l, а в силу непрерывности на границе интервала также обращается в нуль:
[ x < 0
J ^ у = 0. (21.24)
x > I
| Рис.21.6 |
| где U = 0: |
d 2у 2m
2 + —E ■у = 0. dx h
| 2 m ■ E 2 |
| (21.25) |
| (21.26) |
Тогда
d 2у, 2
—2 + к 2 ■у = 0.
dx 2
Решение этого уравнения имеет смысл записать в виде синуса; тогда автоматически удовлетворим требованию непрерывности волновой функции на левом конце интервала (у (0) = 0):
y(x)= A ■ sin(k ■ x). (21.27)
Должно также выполняться условие: у (l) = A ■ sin(k ■ l) = 0; откуда
к ■ l = p ■ n; k = . (21.28)
Здесь n - квантовое число; оно может принимать значения n = 1, 2, 3,....
Для энергии из (21.25):
/' " '7'' ■ l = p ■ n, En = ^-AL n2. (21.29)
V h 2 2 m ■ l 2
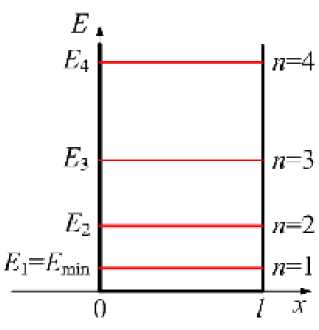
Получено квантование энергии: энергия частицы может принимать только дискретные значения (рис.21.7), которые даёт соотношение (21.29). Минимальное значение энергия принимает при n = 1:
| Emm = E1 = |
| г2„2 n — 2m ■ l 2 ’ |
| Минимальное значение принципа неопределённостей. |
| энергии не может быть равным нулю в силу |
| Рис.21.7 |
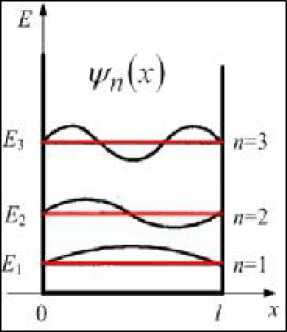
| Из (21.27) и (21.28) волновые функции: |
| При n = 1 |
| при n = 2 |
| при n = 3 |
| Рис.21.8 |
| получим соответствующие этим уровням энергии |
| yn (x) = A ■ sin |
| У1(х)= A ■ sin — |
| (21.30) |
| y 1(x)= A ■ sin — ■ x y2 (x)= A ■ sin 2 — ■ x y3 (x) = A ■ sin 3— ■ x |
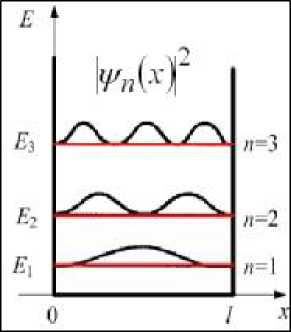
| и т.д. (см. графики функций рис.21.8). Амплитуду А волновой функции находим |
| из условия нормировки (21.15): / l 1У12 ■ dx = 1 ^ J a 2 0 0 |
| ■ sin2 |
| (k l |
| А,. ■ x ■ dx = 1; 0 |
| A 2 l 2 0 |
| ( ( 1 - cos 2 k k |
| ■ x ■ dx = 1 |
| A 2 |
| . (2 — ■ n sin —-— |
| x - |
| АА l ■x k l 0 |
| (2 — ■ n А |
| = 1; |
| ( l - k k |
| ( sin k |
| 2 — ■ n I |
| A ='; |
| Л = jj. (21.31) Расстояние между соседними уровнями энергии из (21.29): *2_ 2 *2_2 *2_2 АЕ„ = E,, +i - Е„ =----------- (п +1)2-------- П = 2 (2п +1). (21.32) 2m ■ l 2 2m ■ l 2 2m ■ l 2 Относительное расстояние между уровнями уменьшается при увеличении квантового числа п: |
| 2 +1 _ АЕп 2п +1 п 2 п = =п ®® 0. E, п2 п п Для больших квантовых чисел п дискретность уровней энергии уже не играет роли; относительное расстояние между ними уменьшается. Это - проявление принципа соответствия: при больших квантовых числах (большая энергия) законы квантовой механики дают тот же результат, что и классическая механика; энергию можно считать изменяющейся непрерывно. Рассчитаем расстояние между уровнями электрона в потенциальной яме шириной: 1) порядка размера атома l»10-10 м: (h 2 2 р 2 |
| энергии при п =1 по (21.32) для |
| h 2 м л ч (6.625 ■Ю-34 Г- 3 -(2п +1) = 2т ■ l 2 8 m ■ l 2^ 8 ■ 9.1 -10-31 ■ 10-20 А Еп = 1.8 -10-17 Дж»100 эВ 2) для макротела размером l» 0.1 м: А Еп = 8 ■ 9.1 ■Ю-31 ■Ю-2 В первом случае дискретность уровней энергии существенна; во втором случае уровни так близки, что энергию можно считать изменяющейся непрерывно. |
| 22 h р АЕп = 2 2 m ■ l 2 |
| 8.3. Линейный гармонический осциллятор 8.3.1. Классический |
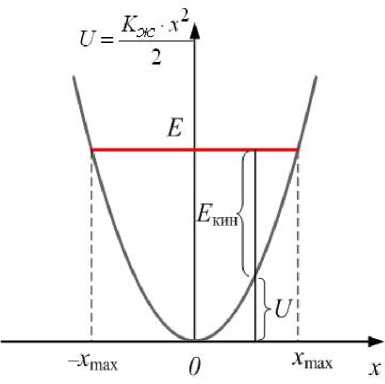
| Классический гармонический осциллятор - это, например, грузик массой m на пружинке жёсткостью Kж. Он колеблется под действием силы упругости в |
| потенциальном поле вида (рис.21.9): |
| (21.33) |
| Полная энергия сохраняется; потенциальной и кинетической: |
| 2 она только перераспределяется между |
| + m v2 = Kж • x max 2 2 |
| (21.34) |
Максимальное смещение грузика определяется запасом полной энергии системы. Координата x изменяется в пределах:
- x max £ x £ x max •
| закону: |
| Рис.21.9 |
с циклической частотой, определяемой параметрами системы - массой груза и
жёсткостью пружины:
| К = mm2. |
—;
m
Поскольку в поворотных точках при x = ± x max скорость v обращается в нуль, вблизи
этих точек грузик движется медленно; так что вероятность обнаружения грузика при x = ± x max
максимальна.
8.3.2. Квантовый гармонический осциллятор
Потенциальную энергию квантового осциллятора возьмём в том же виде, как
и для классического осциллятора.
и (x) = Кж^-; Кж = mw o2.
Здесь величина Кж может быть, например, жёсткостью упругих связей ядер в молекуле; а т - масса ядра. Запишем одномерное стационарное уравнение Шрёдингера с такой потенциальной функцией:
d ' 2т L mm2 • x 21 п
^+^| Е —2 ' =0. ( )
Решать это уравнение мы не будем; приведём результаты. Уравнение (21.35) имеет решение не при любых значениях полной энергии Е, а только при:
| (21.36) |
где и - колебательное квантовое число, принимающее целочисленные значения и = 0, 1,2, 3,
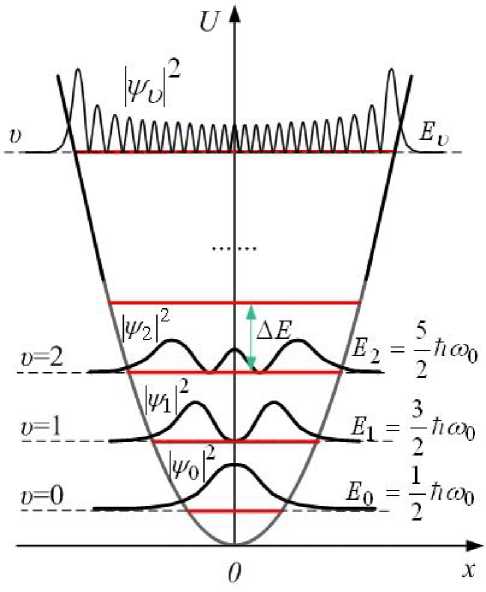
Полная энергия не может обращаться в ноль; её минимальное значение в h mo
основном состоянии системы при и = 0 равно E mjn = E o = —2. Это - так называемые нулевые колебания, следствие принципа неопределённостей. Волновая функция основного состояния выглядит так:
| У 0 °w\v=Q = A ■e 2 h |
| mw0 2 ^x |
| Рис.21.10 |
| на одинаковом расстоянии |
(рис.21.10), равном
DE = Eu+i — Еи = h&o (u +1) + — — h&o u + — 2 0
Переходы этой колебательной системы возможны только между соседними уровнями; при этом излучается или поглощается энергия, равная D E = hw0. На рис.21.10 приводятся также графики Уи |2 - квадрата модуля волновой функции (плотности вероятности) для
соответствующих состояний. Видно, что:
1) Вероятность найти частицу за пределами потенциальной ямы в области, запрещённой классической механикой, отлична от нуля, хотя и быстро убывает.
2) Для больших квантовых
чисел вблизи поворотных точек амплитуда волновой функции
максимальна, то есть вероятность найти в них частицу максимальна, как и в классическом рассмотрении. Это
работает принцип соответствия.
| 8.4. Ангармонический квантовый осциллятор В общем случае любая функция, в том числе и потенциальная энергия как функция координаты х, раскладывается в ряд: (. 2ТТ 1 |
| 1 f d3U ) 3 k ах 3 0 Начало отсчёта можно выбрать так, что U (0) = 0. Пусть х = 0 - точка |
| U (х)= |
| f dU 1 k ах 0 |
| 1 d U ■ х +----- х =0 2 k ах |
| ...•2 |
| ■ х 2 +- |
| ■ х +.... |
| х =0 |
| минимума энергии; тогда |
| f z 1 k ах 0 |
| = 0. х =0 |
| Ограничимся двумя первыми |
ненулевыми членами ряда:
| (21.37) |
| причём обычно в реальных |
системах m << K. Будем решать одномерное
уравнение Шрёдингера с потенциальной функцией (21.37):
| 3 A A m - x 3 00 |
| -y = 0. |
+ E -
dx 2 h 2 ^ к 2
| Рис.21.11 |
| отличные от (21.36): |
| Eu |
| = hw0 |
(1 A2
+ a u + -
к 2 0 0
а расстояния между уровнями энергии неодинаковы:
E = Eu+1 - Еи = hw0(1 + 2a(u +1)).
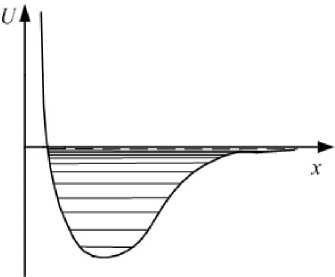
Для молекул коэффициент ангармоничности а<0, то есть уровни энергии «сбегаются» кверху: чем больше энергия, тем ближе уровни друг к другу (рис.21.11); чем дальше от дна потенциальной ямы, тем заметнее отличие энергии ангармонического осциллятора от энергии гармонического.
Туннельный эффект
Физическая энциклопедия даёт такое определение: туннельный эффект (туннелирование) - квантовый переход системы через область движения, запрещённую классической механикой.
Существование туннельного эффекта объясняет альфа-распад атомных ядер. Без туннельного эффекта термоядерная реакция протекала бы при существенно б о льших температурах. Наконец, туннельный эффект играет важную роль в физике твёрдого тела: электроны движутся в периодическом потенциальном поле кристаллической решётки, проникая за счёт туннельного эффекта через барьеры, разделяющие потенциальные ямы.
На примере с гармоническим осциллятором мы уже видели, что квантовая частица с ненулевой вероятностью может быть обнаружена в области, где классическая частица находиться не может (рис.21.10).
| 'U (х) = 0 'и (х) = U 0 |
| (21.38) |
; e < и0.
при 0 < х < l
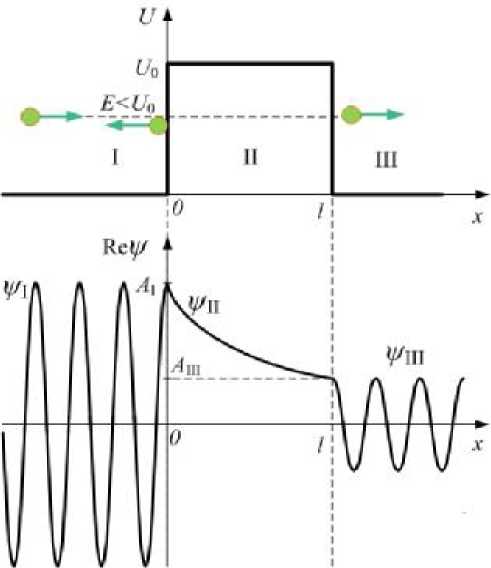
Классическая частица отразится от барьера. Как будет вести себя квантовая? Решая уравнение Шрёдингера с условием (21.38), можно получить волновую функцию частицы. Для области I действительная часть волновой функции: Re y i(х) = Ai - cos(k i - х); Ai - амплитуда волновой функции; ki = ^^E -
\h 2 ,? 2 m i.k
волновое число, причём к2 = — E > 0. Для области II: у ц (х)= А - e1 k l1, где волновое число - мнимая величина: k 2 = —~m (E - U 0) < 0. Введя действительную
| величину b = ~m (U 0 - E) = -i ■ кц \h 2 |
| Рис.21.12 |
| > 0, можно записать решение: y n(х)= A ■ e~b'x, где в силу непрерывности волновой функции в точке х =0 амплитуда A = A j. В области III действительная часть волновой функции: Re У ш (х) = A m ■ cos(k j ■ х). Опять же из-за непрерывности волновой функции в точке x=l можно найти амплитуду A III: ylll(l) = y ll( l); A III = A I ■ e bl • В области II под потенциальным барьером волновая функция уменьшается по экспоненте, то есть достаточно быстро; однако в ноль не обращается: A m ф 0. Это значит, что с ненулевой вероятностью частица проникнет сквозь барьер. Вводится понятие прозрачности барьера: это |
| есть |
| вероятность прохождения частицы под барьером: |
| A III |
| A I |
| 2 = e - 2bl = e |
| ^2m^U0 - E |
отношение квадратов амплитуд волновых функций после и до барьера, то
| Рис. 21.13 |

| E>U0 |
| Квантовая частица |
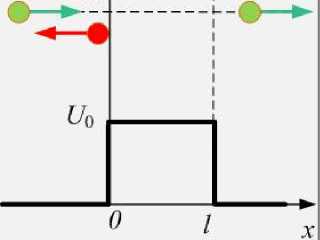
Для микрочастиц есть ещё один эффект:
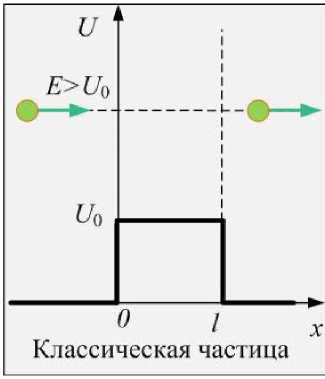
надбарьерное отражение. Если классическая частица пролетит свободно над барьером высотой,
м е ньшей, чем её полная энергия (рис.21.13), то квантовая частица с ненулевой вероятностью отражается от такого низкого барьера.
 2020-07-01
2020-07-01 581
581






