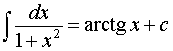Неопределенный интеграл.
Множество всех первообразных функции f (x) называют неопределенным интегралом от функции f (x) и обозначают
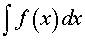
| (1) |
Произносится следующим образом: «Неопределенный интеграл от функции f (x) по dx».
Если F (x) является первообразной f (x), то отсюда следует, что - >

| (2) |
Однако для упрощения данную формулу принято записывать в виде
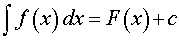
| (3) |
(подразумевая, но не указывая специально, что c – любое число)
В последней формуле f (x) называют подынтегральной функцией, выражение f (x) dx нызывают подынтегральным выражением, а число c называют постоянной интегрирования.
Операцию вычисления (взятия) интеграла по известной подынтегральной функции называют интегрированием функции.
Правила интегрирования. Замена переменной в неопределенном интеграле.
Вычисление интегралов (интегрирование) основано на применении следующих правил:
Правило 1 - интеграл от произведения числа на функцию
Справедливо равенство
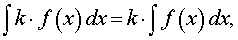
где k – любое число.
Другими словами, интеграл от произведения числа на функцию равен произведению этого числа на интеграл от функции.
Правило 2 - интеграл от суммы функций
Интеграл от суммы функций вычисляется по формуле
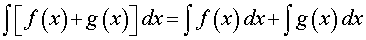 ,
,
то есть интеграл от суммы функций равен сумме интегралов от этих функций.
Правило 3 - интеграл от разности функций
Интеграл от разности функций вычисляется по формуле
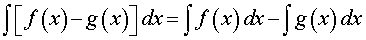 ,
,
то есть интеграл от разности функций равен разности интегралов от этих функций.
Правило 4 - интегрирование при помощи замены переменной
Из справедливости формулы
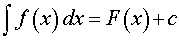
вытекает, что
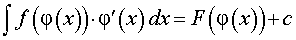
| (4) |
если все входящие в формулу функции f (φ (x)), φ'(x), F (φ(x)) определены.
Доказательство правила 4.
Воспользовавшись формулой для производной сложной функции, вычислим производную от правой части формулы:

Мы получили подынтегральную функцию из левой части формулы, что и требовалось доказать.
Замечание.
Рассмотрим частный случай формулы, когда функция φ(x) является линейной функцией, то есть
φ (x) =kx + b,
что k и b – произвольные числа, 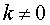 .
.
В этом случае
φ' (x) =k,
и формула принимает следующий вид
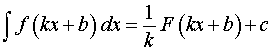
| (5) |
Выведенную нами с вами последнюю с вами формулы мы выведем в соответствующем виде.
Она используется при решении задач на нахождение неопределенного интеграла.
Пример:
Вычислить интеграл
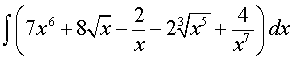
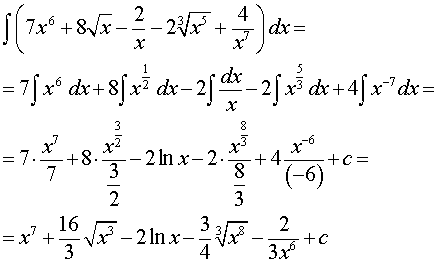
Ответ.
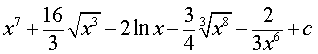
Материал 2. Вспомогательные инструменты для решения задач.
Таблица интегралов
| Основная формула | Обобщения |
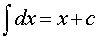
| 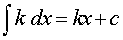 , где k – любое число , где k – любое число
|
|
где n – любое число, не равное – 1 | 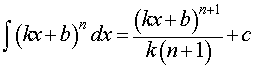 ,
где n, k, b – любые числа, ,
где n, k, b – любые числа, 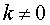 , , 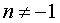
|
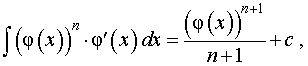 где n – любое число,
где n – любое число, 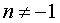
| |
|
| 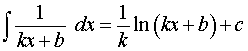 ,
где k, b – любые числа, ,
где k, b – любые числа, 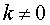 , kx + b > 0 , kx + b > 0
|
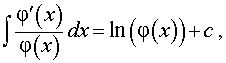 Где φ (x) > 0
Где φ (x) > 0
| |
|
| 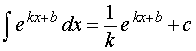 ,
где k, b – любые числа, ,
где k, b – любые числа, 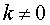
|
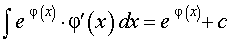
| |
|
где a – любое положительное число, не равное 1 | 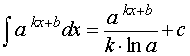 ,
Где a – любое положительное число, не равное 1, k, b – любые числа, ,
Где a – любое положительное число, не равное 1, k, b – любые числа, 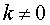
|
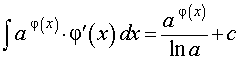 ,
Где a – любое положительное число, не равное 1 ,
Где a – любое положительное число, не равное 1
| |
|
|  ,
где k, b – любые числа, ,
где k, b – любые числа, 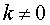
|

| |
|
| 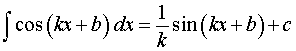 ,
где k, b – любые числа, ,
где k, b – любые числа, 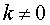
|
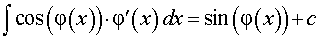
| |
|
| 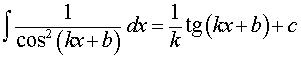 ,
где k, b – любые числа, ,
где k, b – любые числа, 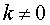 , , 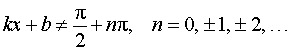
|
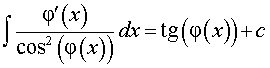 , ,
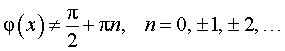
| |
|
| 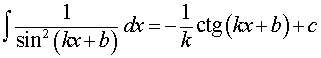 ,
где k, b – любые числа, ,
где k, b – любые числа, 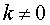 , , 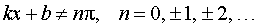
|
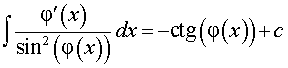 , ,
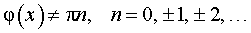
| |
|
| 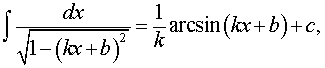 где k, b – любые числа,
где k, b – любые числа, 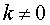 , | kx+b |<1 , | kx+b |<1
|
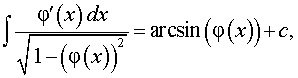 |φ(x)|<1
|φ(x)|<1
| |
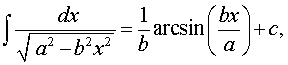 где a, b – любые числа,
где a, b – любые числа, 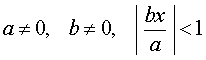
| |
|
|  ,
где k, b – любые числа, ,
где k, b – любые числа, 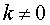
|
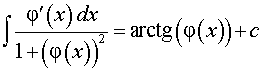
| |
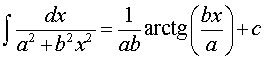 где a, b – любые числа,
где a, b – любые числа, 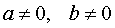
|
Материал 3. Задания для самостоятельной подготовки.
Задание 1.
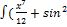 x)dx
x)dx
Задание 2.

Задание 3.
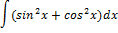
Задание 4.
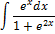
Задание 5.
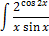
Что необходимо:
1. Данную лекцию (кроме таблицы) необходимо переписать в тетрадь.
2. Лекцию сфотографировать и отправить до 17/04/2020 до 19:00 на https://vk.com/pianom
3. Решить задания для самостоятельной подготовки.
4. Задания также отправить по указанному адресу до 19/04/2020 12:00.
 2020-07-01
2020-07-01 82
82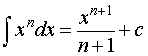
 , x > 0
, x > 0



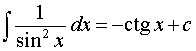
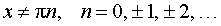
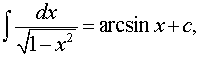 | x |<1
| x |<1