2020-07-01
108
В приближении геометрической оптики поле распространяется вдоль лучей. При таком подходе перенос поля – это перенос комплексной амплитуды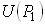 
из точки 
в точку 
.
Уравнение переноса эйконала:
|
Для переноса вещественной амплитуды рассмотрим лучевую (световую) трубку, которая состоит из бесконечно малой площадки 
, и бесконечно узкого пучка лучей – нормалей к волновому фронту. Пучок вырезает на поверхности бесконечно малую площадку 
.
Уравнение переноса вещественной амплитуды:
|
где 
– коэффициент пропускания по энергии между точками.
Уравнение переноса комплексной амплитуды:
|
Функция комплексного пропускания среды вдоль луча 
между точками и характеризует среду между точками и :
|
В рамках геометрической оптики происходит поточечный перенос поля, то есть каждый луч переносит энергию независимо от других лучей. Поле в точке определяется только точкой .
Пределы применимости геометрической оптики
Основное приближение геометрической оптики – это приближение коротких длин волн. Геометрическая оптика не описывает распределение светового поля в следующих ситуациях:
- вблизи предмета и изображения в оптических системах, то есть там, где возможна тонкая структура неоднородностей,
- вблизи фокусов пучков.
В этих случаях требуются другие подходы к описанию светового поля, основанные на теории дифракции.
5. Геометрическая теория оптических изображений. Идеальные оптические системы
Описание оптических систем
