Краткие теоретические сведения

Методические указания

К практическим работам

по дисциплине                  Математика

                                  наименованиедисциплины

 

 

                                                         

Практическая работа 11

Решение тригонометрических уравнений

Цель работы

1.1Обобщить изученный материал по теме.

1.2Выработать умение решать тригонометрические уравнения.

Разделы и темы рабочей программы, которые необходимо знать при выполнении и сдаче практической работы

Разделы 5. Тригонометрические функции числового аргумента.

Краткие теоретические сведения

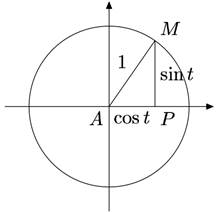рис.1

Определение 1 Синусом угла 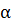 называется ордината точки  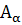угла на тригонометрическом круге, соответствующей числу угла 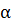. Обозначают ;

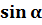                              Косинусом угла 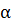 называется абсцисса точки на тригонометрическом круге, соответствующей числу 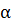. Обозначают .

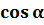                            Тангенсом угла 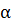 называется отношение ординаты точки  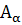к ее абсциссе. Обозначают .

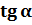                            Котангенсом угла 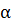 называется отношение абсциссы точки  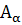к ее ординате. Обозначают .

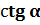Определение 2 Арксинусом числа m называется такое угол х, для которого sin x = m, Обозначают arcsin m.

                     Арккосинусом числа m называется такое угол х, для которого cos x = m, 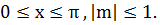Обозначают arcсоs m.

                     Арктангенсом числа m называется такой угол x, для которого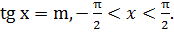

                    Арккотангенсом числа m называется такой угол x, для которого .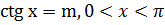

 

Тригонометрические функции связаны между собой основными тождествами:

I. .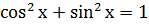

II.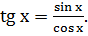

III.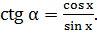

IV. .

V. .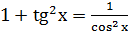

VI. .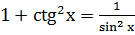

 

Определение 3 Уравнение называется тригонометрическим, если неизвестная величина входит в него как аргумент тригонометрической функции. Решить тригонометрическое уравнение - это значит найти все его корни.

             Простейшими тригонометрическими уравнениями называются уравнения sin x = m, cos x = m, 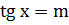, , 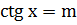где m – данное число.

Формулы корней простейших тригонометрических уравнений:

Уравнение	Общее решение (корни)	Формула №
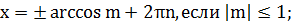
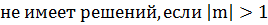
cos x = m		(1)
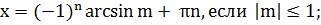
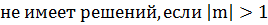
sin x = m		(2)
tg x = m		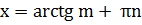(3)
ctg x = m		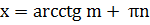(4)

В формулах (1) – (4) n – любое действительное число.

Однородным тригонометрическим уравнением первой степени называется уравнение вида:

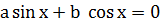
Для его решения обе части уравнения делим на 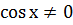. При по членном делении получим уравнение вида:

 (*)

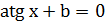Преобразовывая уравнение (*) получаем простейшее уравнение:

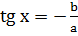, где .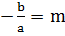

Однородным тригонометрическим уравнением второй степени называется уравнение вида:

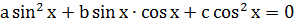
Для его решения обе части уравнения делим на 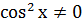. При по членном делении получим уравнение:

 (**)

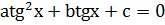Уравнение (**) сводится к квадратному с помощью подстановки .

При решении тригонометрических уравнений используют основные формулы тригонометрии.

Задания

4.1 Изучить методические указания к выполнению практической работы.

4.2 Выполнить индивидуальное задание.

4.3 Оформить отчет по практической работе.

Структура отчета

5.1 Номер и наименование практической работы.

5.2 Цель работы.

5.3 Задание.

5.4 Выполнение работы.

6 Пример выполнения задания

Задача 1. Решите простейшие тригонометрическое уравнение: .

Решение: Согласно формуле (1) находим: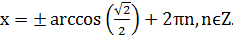

Задача 2. Решите простейшие тригонометрическое уравнение:

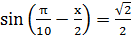
Решение: Функция синус нечетна. Поэтому 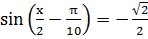. По формуле (2)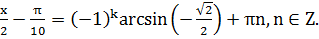

Так как 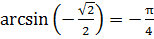, имеем: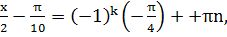

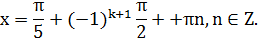
Задача 3. Решите уравнение: 2 sin x+ 3 cos x = 0.

Решение:

2 sin x+ 3 cos x = 0 |: cos x ≠ 0

2 tg x + 3 =0

tg x = -1,5

х= arctg (-1,5) + πk, k 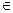Z или х = - arctg 1,5 + πk, k  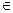 Z

Ответ: - arctg 1,5 + πk, k 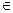  Z.

Задача 4. Решите уравнение: 2 sin² х - 3 sinх cos х - 5 cos²х =0 

Решение: 2 sin² х - 3 sinх cos х - 5 cos²х =0

2 sin² х - 3 sinх cos х - 5 cos²х =0 |: cos²х ≠ 0

2 tg ²x - 3 tg x - 5 = 0

замена tg x = t

2 t² – 3 t – 5 =0

t₁ = -1; t₂  = 2,5

Решением уравнения tg х = -1 являются числа вида х = -π/2 + πk, k 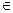  Z.

Решением уравнение tg х = 2,5 являются числа вида х = arctg 2,5+ πn, n 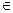 Z.

Ответ: -π/2 + πk, arctg 2,5+ πn, n, k 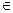  Z.

Задача 5. Решить уравнение 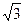sin x + cos x = 1

Решение: 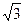sin x + cos x = 1

 

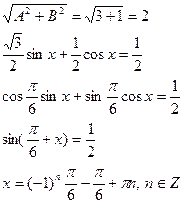
Ответ: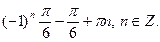

Задача 6. Решите уравнение: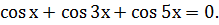

Решение: Группируя первый и последний члены и применяя формулу суммы косинусов, получим

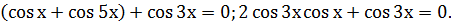
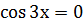Следовательно,  Решая уравнение , находим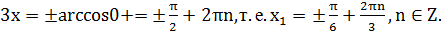

Задача 7. Решите уравнение: sin² х + 5 sin х - 6 =0.

Решение: Введем замену sin х = z, 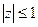, решая квадратное уравнение

 z² + 5 z - 6 = 0, находим z₁ = 1; z₂  = -6 (не удовлетворяет условию )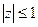

Решением уравнения sin х = 1 являются числа вида х = π/2 +2 π k, k 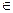 Z.

Ответ: π/2 +2 π k, k  Z.

 

Приложение 1