Формфактор и структура

    Цель этого раздела – понять, каким образом мы получаем информацию о форме и строении объекта, который мы “рассматриваем”. Пусть, для определенности, мы облучаем объект параллельным монохроматическим пучком одинаковых частиц – фотонов, электронов, нейтрино, протонов, нейтронов… Будем рассматривать только абсолютно упругие столкновения, меняющие только направление движения частиц. При этом некоторые частицы могут превращаться в своих партнеров, например, нейтрино в результате взаимодействия посредством заряженного тока превращается в электрон или мюон и т.д. Даже протон, рассеиваясь на нейтроне, может поменяться с ним зарядом (проекцией изоспина). Может меняться и проекция спина (поляризация0. Мы, для упрощения, не будем учитывать подобные эффекты. Таким образом, единственной информацией будет количество частиц (поток), рассеянных в единицу времени в определенный телесный угол 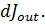 Отношение этой величины к плотности потока налетающих частиц  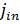есть дифференциальное сечение рассеяния. Это сечение зависит только от угла рассеяния и от энергии налетающих частиц. Наш глаз (в случае монохромного света) получает именно эту информацию, а далее мозг, обрабатывая эту информацию, создает образ рассматриваемого объекта. Что именно делает мозг в этом процессе мы сейчас и постараемся описать.

    Рассмотрим стационарный поток частиц, налетающих вдоль оси OZ на бесконечно тяжелый рассеивающий центр. Потенциал взаимодействия 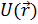считаем финитным. Стационарное уравнение Шредингера

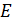y 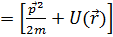y.           (1)

Оператор импульса энергия на бесконечности 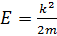. Уравнение (1) запишем в виде

y 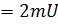y.          (2)

Решение этого уравнения на минус бесконечности (в отсутствии потенциала) находим, с учетом начальных условий, в виде

y _in 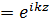                 (3)

Решение уравнения (2) будем искать в виде

y= 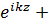 y _out,

где y _out – решение уравнения (2), убывающее на бесконечности.

Функция Грина 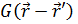для оператора  имеет вид

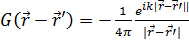 .            (4)

Формальное решение уравнения (2) имеет вид

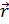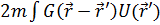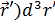y _out ()=  y( (5)

Подынтегральное выражение отлично от нуля в малой окрестности рассеивающего центра, а функция y _out (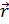) нам нужна будет далеко от рассеивающего центра в области детектора рассеянных частиц. В связи с этим можно разложить функцию Грина в ряд по малому параметру .

Прежде всего заметим, что .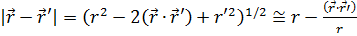

Вводя обозначение 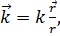 можно представить функцию Грина (4) в виде

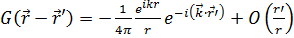 .          (6)

Теперь

y _out (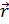)=  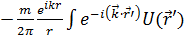y(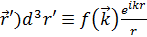         

где 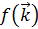- амплитуда рассеяния

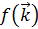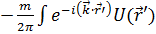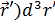=  y(         (7)

Знание амплитуды рассеяния позволяет вычислить дифференциальное сечение рассеяния

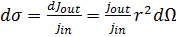                (8)

Здесь 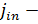 плотность потока налетающих частиц,  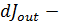поток рассеянных частиц в телесный угол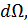 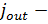 плотность потока рассеянных частиц,  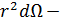поперечное сечение потока рассеянных частиц.

Плотность потока частиц в квантовой механике определяется соотношением

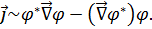
Для налетающих частиц

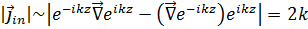
Для рассеянных частиц

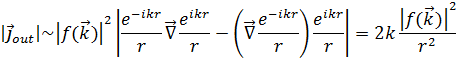
Учтем, что величина вектора 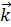 однозначно связана с энергией а направление задается направлением рассеяния, то есть углами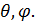

Окончательно дифференциальное сечение рассеяния представим в виде

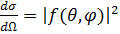                  (9)

Продолжим вычисление амплитуды рассеяния (7):

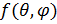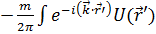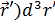=  y(           (10)

В первом (борновском) приближении можно подставить в правую часть выражения (10) волновую функцию y(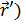 в нулевом приближении  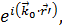где

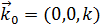
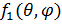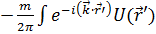
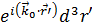=      (11)

Начальный импульс минус конечный – это «переданный» импульс

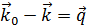
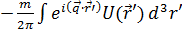=          (12)

Потенциал взаимодействия конкретного поля (сильного, электромагнитного, слабого) определяется как видом соответствующей функции Грина 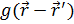, так и распределением плотности источника этого поля:

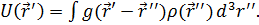        (13)

Подставим выражение для потенциала (13) в формулу амплитуды рассеяния (12) и сделаем замену переменных интегрирования :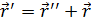

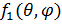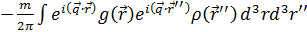=             (14)

Интеграл в выражении (14) факторизовался:

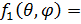F (q) F (q)

F ()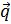

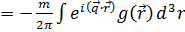
F (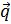)                (15)

Выражение (15) и есть формфактор – Фурье-образ плотности распределения источника поля в рассеивающем центре. Обратное Фурье-преобразование формфактора и даст нам искомую плотность, то есть информацию о структуре рассматриваемого объекта!

Но мы еще не выделили формфактор в явном виде. Ведь экспериментально наблюдаемое сечение рассеяния

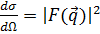| F (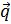)|²           (16)

Прежде, чем двигаться дальше, рассмотрим Фурье-образы различных распределений плотностей. (Смотрите таблицу 6.1 на стр. 161 «Субатомной физики» и читайте пар.5 гл.6).

Бесструктурные (точечные) частицы имеют дельтаобразную плотность 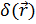 и, соответственно, единичный формфактор. Это дает возможность теоретически вычислить второй сомножитель в выражении (16):

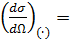| F (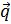)|²         (17)

Теперь, сравнивая экспериментальное сечение рассеяние с сечением, теоретически рассчитанным для данного типа взаимодействия, получаем формфактор реального объекта

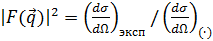         (18)

Для усвоения данной темы рекомендую прочитать в «Субатомной физике» в главе 6 параграфы 1, 2, 3, 4, 5 и параграф 9 до стр.187.

Для самопроверки решите задачи:

1. Нормируя распределение плотности на единицу 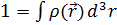, найдите параметр 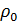в плотностях в таблице 6.1 на стр.161.

2. Рассчитайте максимальную потерю энергии альфа-частицей с энергией 10 МэВ, падающей на покоящийся электрон.

3. Электрон с энергией 100 МэВ рассеивается на ядре свинца. Вычислите максимально возможный переданный импульс, рассчитайте энергию отдачи ядра при заданном значении переданного импульса.