Теоретический материал для самостоятельного изучения

Введем понятия симметричных точек относительно точки, прямой и плоскости.

 

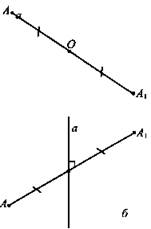
а) Точки А и A1 называются симметричными относительно точки О (центр симметрии), если О - середина отрезка АА1. Точка О считается симметричной самой себе.

Точки А и А1 называются симметричными относительно прямой а (ось симметрии), если прямая а проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка прямой а считается симметричной самой себе.

Точки А и А1 называются симметричными относительно плоскости а (плоскость симметрии), если плоскость а проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка плоскости а считается симметричной самой себе.

б) Итак, точка называется центром симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет центр симметрии, то говорят, что она обладает центральной симметрией.

 

 

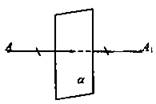
в) Прямая называется осью симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет ось симметрии, то говорят, что она обладает осевой симметрией..

г) Плоскость называется плоскостью симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет плоскость симметрии, то говорят, что она обладает зеркальной симметрией.

Рисунки 78-80 учебника дают наглядное представление о рассматриваемых понятиях.

2) Понятие правильного многогранника

Выпуклый многогранник называется правильным, если все его грани - равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.

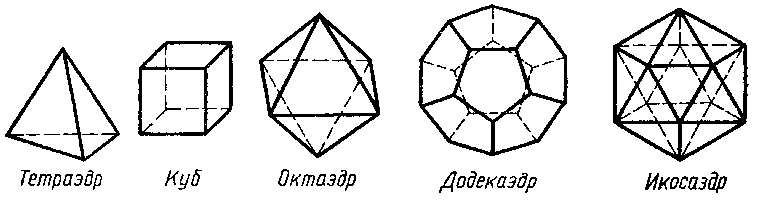В трёхмерном евклидовом пространстве существует всего пять правильных многогранников^[1] (упорядочены по числу граней):

 

Изображение	Правильный многогранник	Число вершин	Число рёбер	Число граней	Число сторон у грани	Число рёбер, примыкающих к вершине	Тип пространственной симметрии
	Тетраэдр	4	6	4	3	3	T d
	Гексаэдр	8	12	6	4	3	O h
	Октаэдр	6	12	8	3	4	O h
	Додекаэдр	20	30	12	5	3	I h
	Икосаэдр	12	30	20	3	5	I h

Название каждого многогранника происходит от греческого наименования количества его граней и слова «грань».

Пусть при одной вершине сходится n ребер, тогда плоских углов при этой вершине будет тоже n, причем они все равны между собой. Пусть один из этих плоских углов равен α, тогда сумма плоских углов при вершине n · α, и по свойству плоских углов многогранного угла получим n · α < 360°, откуда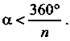

Угол правильного n-угольника равен 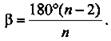Начиная с n = 7 плоский угол станет меньше 60°, а такого правильного многоугольника не существует.

1) Грани правильного многогранника - правильные треугольники, тогда р = 60°.

а) 60° · 3 = 180° < 360°. В этом случае правильный многогранник имеет 4 грани и называется правильным тетраэдром (рис. 81 учебника).

б) 60° · 4 = 240° < 360°. В этом случае правильный многогранник имеет 8 граней и называется правильным октаэдром (рис. 82 учебника).

в) 60° · 5 = 300° < 360°. В этом случае правильный многогранник имеет 20 граней и называется правильным икосаэдром (рис. 83 учебника).

г) 60° · 6 = 360°, это противоречит свойству о сумме плоских углов многогранного угла. Следовательно, больше правильных многогранников, грани которых - правильные треугольники, не существует.

2) Грани правильного многогранника - правильные четырехугольники (квадраты), тогда β = 90°.

а) 90° · 3 = 270° < 360°. В этом случае правильный многогранник имеет 6 граней и называется правильным гексаэдром (кубом) (рис. 84 учебника).

б) 90° · 4 = 360°, следовательно, больше правильных многогранников, грани которых квадраты, не существует.

3) Грани правильного многогранника - правильные пятиугольники, β = 108°.

а) 108° · 3 = 324° < 360°. В этом случае правильный многогранник имеет 12 граней и называется правильным додекаэдром (рис. 85 учебника).

б) 108° · 4 > 360°, следовательно, больше правильных многогранников, грани которых - правильные пятиугольники, не существует.

4) Начиная с правильного шестиугольника β ≥ 120°. Следовательно, n · β > 360° (n ≥ 3), поэтому правильных многогранников, грани которых - многоугольники с числом сторон больше 5, не существует.

Все эти типы многогранников были известны в Древней Греции - именно им посвящена завершающая, XIII книга «Начал» Евклида. Их называют также «платановыми телами» - они занимали видное место в идеалистической картине мира древнегреческого философа Платона. Четыре из них олицетворяют в ней четыре «сущности», или «стихии»: тетраэдр - огонь, икосаэдр - воду, куб - землю, октаэдр - воздух. Пятый же многогранник, додекаэдр, воплощал в себе «все сущее», символизировал все мироздание, почитался главнейшим. Уже по-латыни в средние века его стали называть «пятая сущность» или quinta essentia, «квинта эссенция», отсюда происходит слово «квинтэссенция», означающее все самое главное, основное, истинную сущность чего-либо.

Решение задач

1) 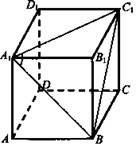Дано: ABCDA1B1C1D1 - куб. А1В и A1C1 - диагонали граней куба, имеющие общий конец.

Найти: ∠ВА1С1.

 

Решение:

1) Пусть а - ребро куба. Так как все грани куба - равные квадраты, то диагонали граней равны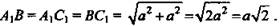

2) ΔA1B1Q - равносторонний, значит, ∠BA1C1 = 60°. (Ответ: 60°.)

 

2) 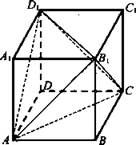Дано: ABCDA1B1C1D1 - куб. D1A, D1C, D1B — диагонали граней.

Доказать: D1AB1C - правильный тетраэдр.

Найти: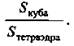

 

Решение:

1) Все грани куба - равные квадраты. Диагонали граней куба, являющиеся ребрами тетраэдра, равны. D1AB1C — правильный.

2) Пусть а - сторона куба. Значит, из ΔАВС: 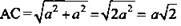- ребро тетраэдра.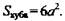

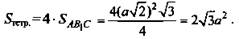
3) 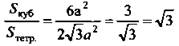(Ответ: √3.)

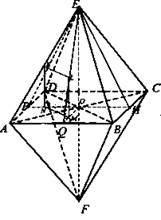
3) Дано: ABCDEF - правильный октаэдр; АВ = а.

Найти: a) BD; б) KL - расстояние между центрами двух смежных граней; в) НМ - расстояние между противоположными гранями.

Решение:

а) Расстояние между противоположными вершинами для всех вершин одинаково. ΔABD - прямоугольный;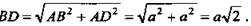

 

 

 

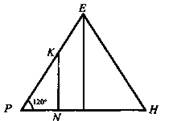
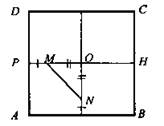
б) Расстояние между центрами двух смежных граней одинаково для всех смежных граней.

1) В грани DEA проведем высоту ЕР, в грани АЕВ проведем высоту EQ. Точки К, L - центры граней. KL - расстояние между центрами граней.

2) В плоскости РОЕ проводим KN ⊥ PO; в плоскости EQO проводим LM ⊥ QО. Тогда MN - проекция искомого отрезка KL на основание, KLMN - прямоугольник.

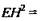
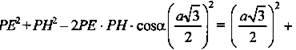
3) В ΔРЕН по теореме косинусов 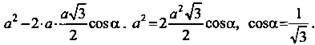ΔЕНВ - прямоугольный.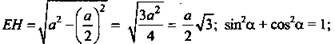

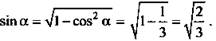
4) РК - радиус окружности, вписанной в правильный ΔEAD.

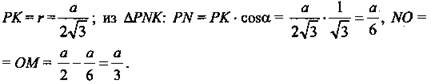
5) ΔNOM - прямоугольный и равнобедренный. 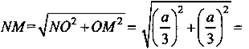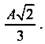Тогда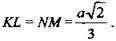

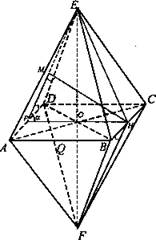в) 1) Проведем через середину квадрата ABCD РН || АВ. FH ⊥ BC, EP ⊥ AD. 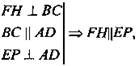грани AED и FBC параллельны

2) Плоскость (РЕН) ⊥ плоскости (FBC). В плоскости (РЕН) проведен отрезок MN ⊥ РЕ.

3) (РЕН) ⊥ AD ⇒ НМ ⊥ AD, НМ ⊥ РЕ, значит, MH ⊥ (AED) и МН ⊥ (FBC). Значит, НМ - искомое расстояние.

4)

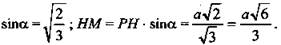
(Ответ: )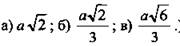

Задача. Высота правильной четырехугольной пирамиды равна 7 см., а сторона основания 8 см. Найдите боковое ребро.

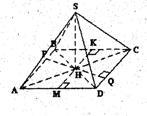Дано: SАВСД– правильная четырех угольная пирамида, SO–высота, SO=7 см, АВ=8см.

Найдите: SА.

Решение.

1.АВСД–квадрат, АС– диагональ, АС= 8 см, АО= 4 см,

2) Треугольник АSО– прямоуг., по теореме Пифагора АS===9(см).

Задача. В правильной четырехугольной пирамиде боковая поверхность равна 14,76 м², а полная поверхность18 м².Найдите сторону основания и высоту пирамиды.

Дано: SАВСД– правильная четырех угольная пирамида,S_{бок. пов=}14,76 м², S_{пол. пов.}=18 м². Найдите: АВ, SO.

Решение.

1. S_{пол. пов-–} S_{бок. пов} = 18–14,76= 3,24(м²)

2.АВСД– квадрат, АВ= 1,8 см., ОК = 0,9 см.

3. S_бок.= Р*L, 14,76 = *4*1,8*SК, SК= 4,1см.,SО= =4(см).