2020-06-29
112
6.4.1. Вычислить несобственный интеграл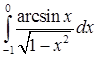 
.
Решение. Интеграл является несобственным, так как подынтегральная функция имеет в точке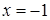 
бесконечный разрыв.
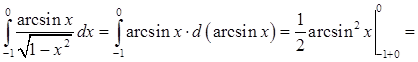
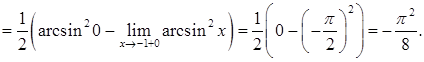
6.4.2. Вычислить несобственный интеграл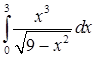 
.
Решение. Интеграл является несобственным, так как подынтегральная функция имеет в точке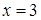 
бесконечный разрыв.
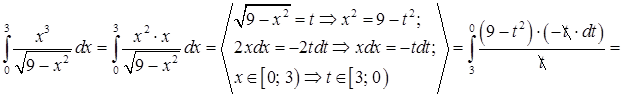
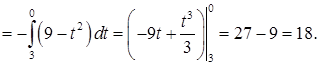
Замечание. В процессе замены интеграл стал определенным.
6.4.3. Вычислить несобственный интеграл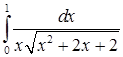 
.
Решение. Подынтегральная функция имеет бесконечный разрыв в точке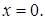 
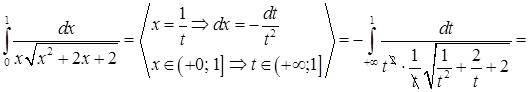
Так как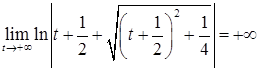 
, то интеграл расходится
Замечание. В результате замены несобственный интеграл от неограниченной функции стал интегралом с бесконечным верхним пределом.
6.4.4. Вычислить несобственный интеграл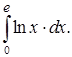 
Решение. Интеграл является несобственным, так как подынтегральная функция имеет в точке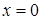 
бесконечный разрыв.
Для вычисления интеграла надо применить интегрирование по частям.
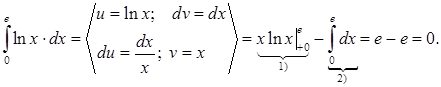
1) 
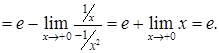2) 
.
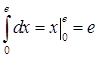6.4.5. Исследовать на сходимость несобственный интеграл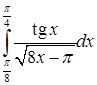 
.
Решение. Функция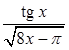 
непрерывна на промежутке 
и имеет бесконечный разрыв в точке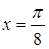 
(нижняя граница интегрирования). Интеграл является несобственным. На указанном промежутке выполняется неравенство 
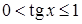. Поэтому подынтегральная функция удовлетворяет условию 
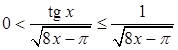. Интеграл от вспомогательной функции 
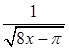сходится:
|
|
|
.
Следовательно, интеграл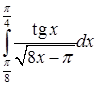 
сходится.
6.4.6. Исследовать на сходимость интеграл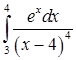 
.
Решение. Функция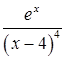 
непрерывна на промежутке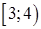 
и имеет бесконечный разрыв в точке 
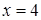(верхняя граница интегрирования). Интеграл является несобственным. На промежутке интегрирования выполняется неравенство 
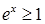и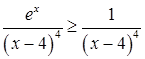 
. Несобственный интеграл от вспомогательной функции 
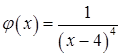расходится:
,
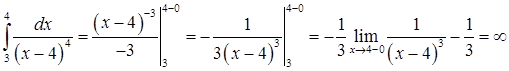следовательно, интеграл 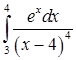расходится.
6.4.7. Исследовать на сходимость интеграл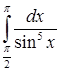 
.
Решение. Сделаем в этом интеграле замену переменной:
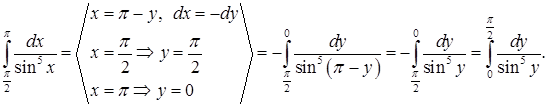
На промежутке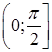 
подынтегральная функция 
.
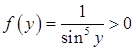В качестве вспомогательной функции можно взять 
, так как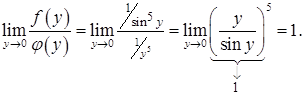 
Интеграл 
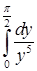расходится по признаку 6.2.4. Следовательно, 
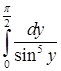также расходится на основании признака 6.3.2.
