Для вычисления несобственного интеграла можно применять замену.
Может случиться, что с помощью замены переменной несобственный интеграл превратится в определенный.
Несобственный интеграл 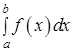 по конечному промежутку
по конечному промежутку 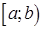 заменой переменной может быть преобразован в интеграл по неограниченному промежутку.
заменой переменной может быть преобразован в интеграл по неограниченному промежутку.
6.2.3. Интегрирование по частям в несобственных интегралах от неограниченных функций.
Пусть 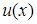 и
и 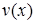 – непрерывно дифференцируемые на промежутке
– непрерывно дифференцируемые на промежутке 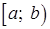 функции.
функции.
Тогда имеет место формула: 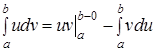
Пусть 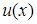 и
и 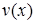 – непрерывно дифференцируемые на промежутке
– непрерывно дифференцируемые на промежутке 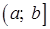 функции.
функции.
Тогда имеет место формула: 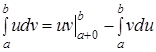 (ср. п. 2.2).
(ср. п. 2.2).
6.2.4. Cходимость несобственного интеграла 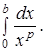
Интеграл 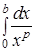 сходится при
сходится при 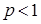 и расходится при
и расходится при 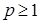 .
.
Признаки сходимости несобственных интегралов
От неограниченных функций
6.3.1. Пусть функции 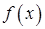 и
и 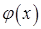 непрерывны при
непрерывны при 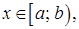 в точке
в точке 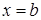 имеют бесконечный разрыв, и на интервале
имеют бесконечный разрыв, и на интервале 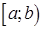 выполняется условие
выполняется условие 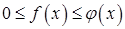 . Тогда:
. Тогда:
1) Если сходится 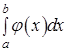 , то сходится и
, то сходится и 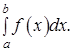
2) Если расходится 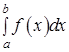 , то расходится и
, то расходится и 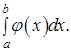
6.3.2. Пусть функции 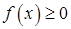 и
и 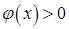 непрерывны при
непрерывны при 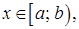 в точке
в точке 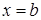 имеют бесконечный разрыв, и выполняется условие
имеют бесконечный разрыв, и выполняется условие
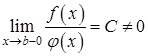 (функции одного порядка; при (функции одного порядка; при 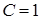 эквивалентны).
Тогда интегралы эквивалентны).
Тогда интегралы 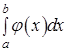 и и 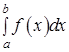 одновременно либо сходятся, либо расходятся. одновременно либо сходятся, либо расходятся.
|
6.3.3.Абсолютная и условная сходимость.
Пусть функция 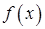 непрерывна при
непрерывна при 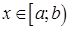 и в точке
и в точке 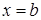 имеет бесконечный разрыв.
имеет бесконечный разрыв.
Если 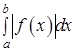 (интеграл от абсолютной величины функции (интеграл от абсолютной величины функции 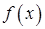 ) сходится, то ) сходится, то 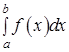 сходится. В этом случае сходится. В этом случае 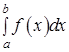 называется абсолютно сходящимся.
Если называется абсолютно сходящимся.
Если 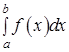 сходится, а сходится, а 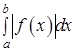 расходится, то интеграл расходится, то интеграл 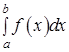 называется условно сходящимся. называется условно сходящимся.
|
 2020-06-29
2020-06-29 155
155








