2020-07-12
685
Молекулы жидкости в объёме и на её свободной поверхности находятся в неэквивалентных условиях (см. рис 3.1).
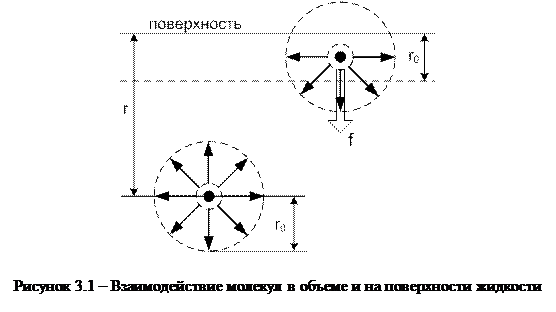
Каждая молекула испытывает притяжение со стороны всех соседних молекул, находящихся в пределах сферы молекулярного действия радиусом r 0, центр которой совпадает с данной молекулой. Равнодействующая всех сил для молекул в объеме жидкости (при r >2 r 0) в среднем равна нулю. В приповерхностной области (при r < r о) окружение каждой молекулы несимметрично и действие соседних молекул не скомпенсировано. Таким образом, на каждую молекулу, находящуюся в приповерхностном слое толщины ~ r 0 действует результирующая сила f, направленная в объем жидкости. Под действием этой силы молекулы совершают более частые переходы в объем. Поэтому в приповерхностном слое концентрация молекул ниже, чем в объеме. Этот слой оказывается как бы растянутым, обладает дополнительной потенциальной (упругой) энергией и ведет себя подобно резиновой пленке, для молекул это означает, что они должны совершить работу против равнодействующей силы f, чтобы перейти из объема в приповерхностный слой.
Макроскопической удельной характеристикой избыточной энергии поверхностного слоя является коэффициент поверхностного натяжения – это его энергетическое определение
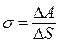, (3.2)
где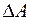 
– работа, затраченная на увеличение свободной поверхности жидкости (поверхностного слоя) на площадь 
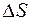. Работа 
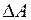идет на увеличение энергии поверхностного слоя, т. е. 
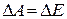. Поэтому из определения коэффициента σ следует, что энергия поверхностного натяжения пленки площадью 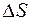равна:
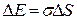. ( 3.3)
Всякая физическая система в состоянии равновесия стремится к минимуму потенциальной энергии. Поэтому, например, капля жидкости в состоянии свободного падения принимает форму шара, мыльный пузырь имеет сферическую форму и т. д., т. к. сфера имеет минимальную площадь поверхности при заданном объеме.
Стремление поверхностного слоя к сокращению приводит к тому, что на границе слоя действует сила. Если на границу пленки жидкости длиной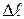 
действует сила Δ F, то при перемещении перпендикулярно границе на расстояние совершается работа 
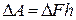. С другой стороны 
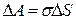,а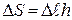 
– изменение площади пленки. Из сравнения этих работ силовое определение коэффициента поверхностного натяжения
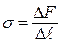, (3.4)
где Δ F – сила, действующая на границу пленки жидкости длиной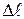 
.
Обратное соотношение позволяет рассчитывать силу поверхностного натяжения
. (3.5)
Необходимо помнить, что это соотношение справедливо для прямолинейного участка границы пленки. Для. криволинейных границ пленки силы Δ F нужно суммировать или в пределе при 
производить криволинейное интегрирование.
Другое важное следствие действия поверхностного натяжения состоит в том, что под искривлённой поверхностью жидкости создаётся избыточное давление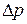 
. Согласно формуле Лапласа его величина
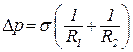, (3.6)
 |
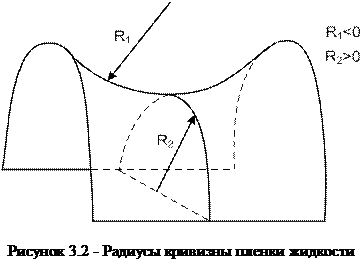где R1 и R2 – радиусы кривизны пленки жидкости в данной точке. Они определяются сечениями поверхности взаимно перпендикулярными плоскостями (см. рис. 3.2) и могут быть как положительными, так отрицательными. Например, для капли жидкости R1=R2=R – радиусу капли и
.
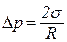Значения коэффициента поверхностного натяжения для некоторыхжидкостей приведены в, таблице 3.1.
Таблица 3.1 – Коэффициенты поверхностного натяжения
| № п/п | Жидкость (20ºС) | Коэффициент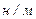  
|
| 1 | Бензин | 21 |
| 2 | Бензол | 41,5 |
| 3 | Вода | 72,75 |
| 4 | Мыльный раствор | 40 |
| 5 | Нефть | 30 |
| 6 | Спирт этиловый | 22,0 |
| 7 | Ртуть | 513 |
| 8 | Фреон-12 | 9,0 |
