План занятия

1. Логические высказывания, связки и операции

2. Переменные и формулы в исчислении высказываний

3. Предикаты. Семантика исчисления предикатов

4. Правила логического вывода

 

Вопрос 1. Логические высказывания, связки и операции

Математическая логика — раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики.

Логика – это наука, которая учит, как нужно правильно рассуждать, правильно делать умозаключения и выводы, получая в результате правильные высказывания. Логика изучает лишь те акты мышления, которые фиксированы в языке в виде слов, предложений и их совокупности.

Методы математической логики широко используются при создании компьютеров (алгебра высказываний и булевы функции – математический аппарат для разработки релейно-контактных схем) и математического обеспечения для них (логика предикатов, теория алгоритмов, экспертные системы).

Основными объектами разделов логики являются высказывания.

Высказыванием называется предложение, к которому возможно применить понятия «истинно» или «ложно».

В математической логике не рассматривается сам смысл высказываний, определяется только его истинность или ложность, что принято обозначать соответственно И или Л.

Пример 1. Рассмотрим суждения: 1) «3<7»; 2) «Волга впадает в черное море»; 3) «Я лгу».

Первое высказывание является истинным, второе – ложным. Третье суждение не является высказыванием, так как ему нельзя присвоить значение «истина» или «ложь».

 

К высказываниям не относятся вопросительные и отрицательные предложения.

Высказывание будем называть простым (элементарным), если оно рассматривается как некое неделимое целое (аналогично элементу множества).

Сложным (составным) называется высказывание, составленное из простых с помощью основных логических связок.

Пример 2. Высказывание «Идет дождь или снег» – сложное, так как состоит из двух простых высказываний: А – «Идет дождь», В – «Идет снег», соединенных связкой «или».

 

Логическим связкам соответствуют логические операции над высказываниями: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность.

Логические значения результатов этих операций связаны с логическими значениями исходных высказываний. Соответствие между высказываниями определяется таблицей истинности.

Пусть даны два произвольных высказывания A и B.

1. Первая логическая операция над этими высказываниями - конъюнкция - представляет собой образование нового высказывания, которое будем обозначать A ∧ B и которое истинно тогда и только тогда, когда A и B истинны. В обычной речи этой операции соответствует соединение высказываний связкой "и".

Таблица истинности для конъюнкции:

A	B	A ∧ B
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

2. Вторая логическая операция над высказываниями A и B - дизъюнкция, выражаемая в виде A ∨ B, определяется следующим образом: оно истинно тогда и только тогда, когда хотя бы одно из первоначальных высказываний истинно. В обычной речи эта операция соответствует соединению высказываний связкой "или". Однако здесь мы имеем не разделительное "или", которое понимается в смысле "либо-либо", когда A и B не могут быть оба истинны. В определении логики высказываний A ∨ B истинно и при истинности лишь одного из высказываний, и при истинности обоих высказываний A и B.

Таблица истинности для дизъюнкции:

A	B	A ∨ B
И	И	И
И	Л	И
Л	И	И
Л	Л	Л

3. Третья логическая операция над высказываниями A и B, выражаемая в виде A → B; полученное таким образом высказывание ложно тогда и только тогда, когда A истинно, а B ложно. A называется посылкой, B - следствием, а высказывание A → B - следованием, называемая также импликацией. В обычной речи эта операция соответствует связке "если - то": "если A, то B". Но в определении логики высказываний это высказывание всегда истинно независимо от того, истинно или ложно высказывание B. Это обстоятельство можно кратко сформулировать так: "из ложного следует всё, что угодно". В свою очередь, если A истинно, а B ложно, то всё высказывание A → B ложно. Оно будет истинным тогда и только тогда, когда и A, и B истинны. Кратко это можно сформулировать так: "из истинного не может следовать ложное".

Таблица истинности для следования (импликации):

A	B	A → B
И	И	И
И	Л	Л
Л	И	И
Л	Л	И

4. Четвёртая логическая операция над высказываниями, точнее над одним высказыванием, называется отрицанием высказывания A и обозначается ~ A (можно встретить также употребление не символа ~, а символа, а также верхнего надчёркивания над A). ~ A есть высказывание, которое ложно, когда A истинно, и истинно, когда A ложно.

Таблица истинности для отрицания:

A	~ A
Л	И
И	Л

5. И, наконец, пятая логическая операция над высказываниями называется эквивалентностью и обозначается A ↔ B. Полученное таким образом высказывание A ↔ B есть высказывание истинное тогда и только тогда, когда A и B оба истинны или оба ложны.

Таблица истинности для эквивалентности:

A	B	A → B	B → A	A ↔ B
И	И	И	И	И
И	Л	Л	И	Л
Л	И	И	Л	Л
Л	Л	И	И	И

В большинстве языков программирования есть специальные символы для обозначения логических значений высказываний, записываются они почти во всех языках как true (истина) и false (ложь).

Вопрос 2. Переменные и формулы в исчислении высказываний

Понятие логической формы сложного высказывания уточняется с помощью понятия формулы логики высказываний.

Для обозначения высказываний, как и упомянутом примере, будем продолжать использовать буквы

p, q, r,..., p1, q1, r1,...

Эти буквы будут играть роль переменных, принимающих в качестве значений истинностные значения "истина" и "ложь". Эти переменные называются также пропозициональными переменными. Мы будем далее называть их элементарными формулами или атомами.

Понятие формулы логики высказываний определим следуюшим образом:

1) элементарные формулы (атомы) являются формулами логики высказываний;

2) если A и B - формулы логики высказываний, то ~A, (A ∧ B), (A ∨ B), (A → B), (A ↔ B) тоже являются формулами логики высказываний;

3) только те выражения являются формулами логики высказываний, для которых это следует из 1) и 2).

Пример 3. Пусть p - одиночное высказывание (атом) "Все рациональные числа являются действительными", q - "Некоторые действительные числа - рациональные числа", r - "некоторые рациональные числа являются действительными". Переведите в форму словесных высказываний следующие формулы логики высказываний:

1) ;

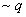2) ;

 

3) ;

4) ;

 

5) ;

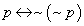6) .

Решение.

1) "нет действительных чисел, которые являются рациональными";

2) "если не все рациональные числа являются действительными, то нет рациональных чисел, являющихся действительными";

3) "если все рациональные числа являются действительными, то некоторые действительные числа - рациональные числа и некоторые рациональные числа являются действительными";

4) "все действительные числа - рациональные числа и некоторые действительные числа - рациональные числа и некоторые рациональные числа являются действительными числами";

5) "все рациональные числа являются действительными тогда и только тогда, когда не имеет место быть, что не все рациональные числа являются действительными";

6) "не имеет места быть, что не имеет место быть, что не все рациональные числа являются действительными и нет действительных чисел, которые являются рациональными или нет рациональных чисел, которые являются действительными".

 

Заметим, что никакой атом не имеет вида ~A, (A ∧ B), (A ∨ B), (A → B), (A ↔ B). Такой вид имеют сложные формулы.

Число скобок в формулах логики высказываний можно уменьшить, если принять, что

1) в сложной формуле будем опускать внешнюю пару скобок;

2) упорядочим знаки логических операций "по старшинству":

↔, →, ∨, ∧, ~.

В этом списке знак ↔ имеет самую большую область действия, а знак ~ - самую маленькую. Под областью действия знака операции понимаются те части формулы логики высказываний, к которым применяется (на которые действует) рассматриваемое вхождение этого знака. Таким образом, можно опускать во всякой формуле те пары скобок, которые можно восстановить, учитывая "порядок старшинства". А при восстановлении скобок сначала расставляются все скобки, относящиеся ко всем вхождениям знака ~ (при этом мы продвигаемся слева направо), затем ко всем вхождениям знака ∧ и так далее.

Пример 4. Восстановите скобки в формуле логики высказываний B ↔ ~ C ∨ D ∧ A.

Решение. Скобки восстанавливаются пошагово следующим образом:

B ↔ (~ C) ∨ D ∧ A

B ↔ (~ C) ∨ (D ∧ A)

B ↔ ((~ C) ∨ (D ∧ A))

(B ↔ ((~ C) ∨ (D ∧ A)))

Не всякая формула логики высказываний может быть записана без скобок. Например, в формулах А → (B → C) и ~ (A → B) дальнейшее исключение скобок невозможно.

Вопрос 3. Предикаты. Семантика исчисления предикатов

Логика предикатов разбивает элементарное высказывание на субъект (подлежащее или дополнение) и предикат (сказуемое или определение). Субъект – это то, о чем что-то утверждается в высказывании, предикат – это то, что утверждается о субъекте.

Пример 5. «7 – простое число». «7» – субъект, «простое число» – предикат. Это высказывание утверждает, что число 7 обладает свойством быть простым.

 

Синтаксис и семантика логики предикатов:

- логическая константа – true (истина) и false (ложь);

- константа – символьное выражение, начинающееся со строчной буквы (например, cat, blue);

- переменная – символьное выражение, начинающееся с прописной буквы или знака подчеркивания (например, X, Сat, _blue);

- функция и предикат – символьное выражение, начинающееся со строчной буквы, за которым следует список аргументов (термов), заключенных в скобки (например, кошка (катя), sin(X), друзья (вася, петя)). Отличие функции от предиката, заключается в том, что функция возвращает результаты любого типа (строку, число, дату и т.д.), а предикат – только логического типа (истину или ложь);

- список – упорядоченный набор элементов (констант, переменных или предикатов), указанных через запятую и заключенных в квадратные скобки (например, [red, blue], [X, Сat, _blue], [кошка(катя)]);

- терм – константа, переменная, функция или список;

- логическая операция:

- (~) – отрицание;

- ∧ (&) – логическое И (конъюнкция, логическое умножение);

- ∨ – логическое ИЛИ (дизъюнкция, логическое сложение);

- → (⇒) – импликация (если - то);

- ↔ (⇔, ≡) – эквивалентность;

- квантор переменной:

- ∃ – квантор существования;

- ∀ – квантор всеобщности;

- вспомогательный символ: круглые скобки, запятые, +, - и т.п;

- формула (предложение, правило, правильно построенная формула) - предикат (атом), логическое выражение или одна из следующих конструкций: А, A∧B, A∨B, A→B, A↔B, (∀X) A и (∃X) A, где A и B - формулы, а X - переменная. Результатом вычисления формулы является либо истина либо ложь.

Приоритет операций и кванторов при исчислении формул показан ниже.

В скобках показаны операции (кванторы) с одинаковым приоритетом. Если в формуле используются операции (кванторы) с одинаковым приоритетом, то порядок исчисления слева-направо. Изменение порядка исчисления можно добиться за счет использования круглых скобок «()».

Примеры формул:

- если Маша мать X и Y, то X является братом или сестрой Y:

мать(маша, X) ∧ мать(маша, Y) → брат(X, Y) ∨ сестра(X, Y).

- если X – человек, то он смертен:

человек(X) → смертен(X).

Квантор существования ∃ указывает, что предложение истинно, по крайней мере, для одного значения переменной. Например, ∃X друзья(X, петя) – существует, по крайней мере, один субъект X, который является другом Пети.

Квантор всеобщности ∀ указывает, что предложение истинно, для всех значений переменной. Например, ∀X человек(X) → смертен(Х) – все люди смертны.

При комбинации кванторов очень важен порядок их использования, например:

- ∀X∃Y любит(Х, Y) – любой Х любит хотя бы одного Y;

- ∀Y∃X любит(Х, Y) – любого Y любит хотя бы один Х;

- ∃X∀Y любит(Х, Y) – существует такой Х, который любит всех Y;

- ∃Y∀X любит(Х, Y) – существует такой Y, которого любят все X;

- ∀X∀Y любит(Х, Y) и ∀Y∀Х любит(Х, Y) – любой X любит всех Y и любой Y любим всеми X (эквивалентные предложения);

- ∃X∃Y любит(Х, Y) – существует такой X, который любит хотя бы одного из Y;

- ∃Y∃Х любит(Х, Y) – существует такой Y, которого любит хотя бы один X.

 

Вопрос 4. Правила логического вывода

Пусть есть высказывания, которые можно назвать посылками. Пусть также есть высказывание, которое можно назвать выводом. Словосочетание "можно назвать" используется при условии, что посылки связываются с выводом. То есть, из посылок логически следует вывод. Тогда, если посылки имеют значения "истина" и вывод тоже имеет значение "истина", то аргумент является валидным. Если же посылки имеют значения "истина", а вывод имеет значение "ложь", то аргумент не является валидным. Синонимы понятия "валидность" (в рассматриваемом здесь значении) - "логическая правильность", "резонность".

Пример валидного аргумента:

Посылка. A и B - программисты

Посылка. A и B разрабатывают программы для бухгалтеров

Вывод. Есть программисты, которые разрабатывают программы для бухгалтеров

То есть, из посылок логически следует вывод.

Пример не валидного аргумента:

Посылка. Запись числа может содержать запятую

Посылка. В предложении может быть запятая

Вывод. Есть числа, которые называются предложениями

То есть, из посылок логически не следует вывод.

 

Пример 6. Проверьте валидность аргумента, если

Посылка.

Посылка.

Вывод.

Решение. Составляем таблицу истинности:

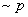
И	И	Л	И	И	И
И	Л	Л	Л	Л	И
Л	И	И	И	И	Л
Л	Л	И	И	И	И

В третьей строке обе посылки истинны, а вывод - ложный. Следовательно, аргумент не валидный. Таким образом, в аналогичных задачах подозрительными являются те строки, в которых все посылки истинны. Если вывод также истинный, то аргумент валидный, если ложный, то аргумент не валидный, как в этом примере. Если же посылки или обе ложны, или ложна одна из них, то такие строки не играют роли в проверке аргумента на валидность, каким бы ни было значение вывода.