Тема: «Числа и алгебраические преобразования»
План
1. Повторение теоретического материала.
1.1. Корни натуральной степени из числа, их свойства.
1.2. Степень с натуральным показателем.
1.3. Степень с целым показателем.
1.4. Формулы сокращённого умножения.
1.5. Разложение многочленов на множители.
2. Решение заданий по теме занятия.
Цели занятия:
1. Систематизировать и обобщить теоретические знания по теме занятия.
2. Совершенствовать навыки решения заданий на преобразование алгебраических, рациональных, иррациональных, степенных выражений с использованием формул сокращенного умножения, основных свойств корней и степеней.
Задачи занятия:
1. Развитие навыков в применении всех способов преобразования алгебраических, рациональных, иррациональных, степенных выражений с использованием формул сокращенного умножения, основных свойств корней и степеней с целью подготовки к успешной сдаче экзамена.
2. Создание условий для развития познавательного интереса к предмету, развития логического мышления и самоконтроля.
3. Развивать основные мыслительные операции обучающихся: умение сравнивать, анализировать.
ПОВТОРЕНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА.
Корни натуральной степени из числа, их свойства.
Корень n – степени: 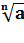 , n - показатель корня, а – подкоренное выражение.
, n - показатель корня, а – подкоренное выражение.
Если n – нечетное число, то выражение 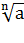 имеет смысл при
имеет смысл при 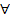 а.
а.
Если n – четное число, то выражение 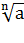 имеет смысл при
имеет смысл при 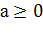 .
.
Арифметический корень: 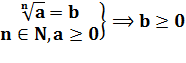
Корень нечетной степени из отрицательного числа: 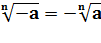
Основные свойства корней.
1. Правило извлечения корня из произведения: 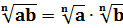
2. Правило извлечения корня из дроби: 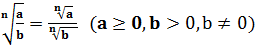
3. Правило извлечения корня из корня: 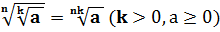
4. Правило вынесения множителя из под знака корня: 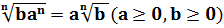
5. Внесение множителя под знак корня: 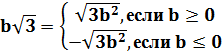 ,
,
6. Показатель корня и показатель подкоренного выражения можно умножить на одно и тоже число. 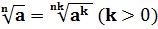
7. Правило возведения корня в степень. 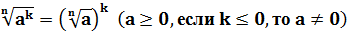
Степень с натуральным показателем.
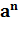 =
= 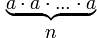 ,a – основание степени, n – показатель степени
,a – основание степени, n – показатель степени
Свойства:
1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается неизменным. 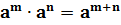
2. При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным. 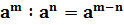
3. При возведении степени в степень показатели перемножаются. 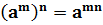
4. При возведении в степень произведения двух чисел, каждое число возводят в эту степень, а результаты перемножают. 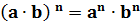
5. Если в степень возводят частное двух чисел, то в эту степень возводят числитель и знаменатель, а результат делят друг на друга. 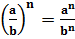
6. Если 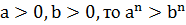
 2020-07-12
2020-07-12 100
100







