2020-07-12
64
Если функция f непрерывна на отрезке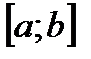 
, то среди ее значений на этом отрезке есть наибольшее и наименьшее.
Чтобы найти наименьшее и наибольшее значения функции f на отрезке 
, надо:
а) найти ее значение на концах этого отрезка (т. е. числа f(а) и f(b));
б) найти ее значения в точках, где производная функции равна нулю;
в) найти ее значения в точках, где функция f не имеет производной;
г) из всех найденных значений выбрать наибольшее и наименьшее.
Решение многих задач практики приводит к отысканию наибольших или наименьших значений некоторой функции на некотором отрезке.
Примеры выполнения заданий.
Пример 1. Исследуйте функцию и постройте график: 
Решение:
1. Область определения функции: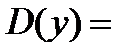 
ℝ.
2. Область значений функции: 
ℝ. (Определяем после построения графика).
3. Точки пересечения с осями координат.
3.1. Нули функции: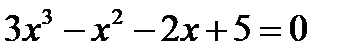 
Данное уравнение решить сложно, поэтому нули функции посмотрим по графику.
3.2. Точки пересечения с осью ОУ: х=0, соответственно у=5.
4. Нахождение критических точек. Определение промежутков возрастания и убывания функции:
|
|
|
ü Найдем производную функции: 
ü 
Приравняем производную к 0, найдем корни уравнения: 
, 
, 
, 
, 
.
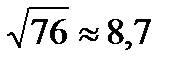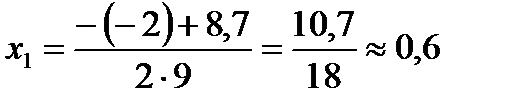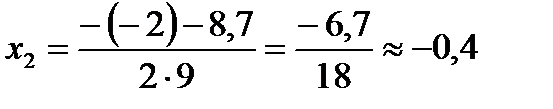ü Исследуем промежутки:
Следовательно:
- функция возрастает,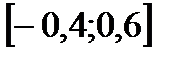 
- функция убывает.
- точка максимума, 
- точка минимума.
5. Исследование функции на выпуклость, вогнутость, определение точек перегиба (исследование проводится по второй производной функции).
ü Найдем вторую производную функции: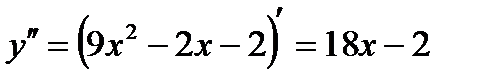 
ü Приравняем к 0, найдем корни уравнения: 
, 
.
ü 
Исследуем промежутки:
ü Следовательно:
- функция выпуклая, 
- функция вогнутая.
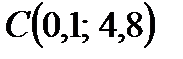- точка перегиба.
6. Функция не периодическая.
7. Четность, нечетность функции.
| 
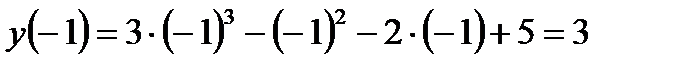
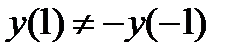
| функция общего вида. |
8. Уточнение графика функции по точкам (произвести окончательное уточнение графика, в особенности на участках, где информация о нем недостаточна).
| х | -1,5 | -1 | -0,4 | 0 | 0,1 | 0,6 | 1 | 1,2 |
| у | -4,4 | 3,0 | 5,4 | 5,0 | 4,8 | 4,1 | 5,0 | 6,3 |
| max | перегиб | min |
9. Построение графика.
