проводимую с 7.07.2020 г. по 20.07.2020 г.
1. Дать определения основным понятиям «Теории автоматического управления»:
· управление, объект управления, устройство управления, воздействие, автоматическая система (АС), непрерывные АС, Модель АС, типовые воздействия АС;
· передаточная функция, переходная функция, переходная импульсная функция, амплитудная частотная характеристика, фазовая частотная характеристика (и соответствующие логарифмические), частота среза;
· типовые динамические звенья, структурно-динамическая схема АС, качество АС;
· устойчивость АС, нуль АС, полюс АС, критерии устойчивости, характеристическое уравнение системы, запас устойчивости, частота сопряжения, время регулирования, время перерегулирования, статическая АС, астатическая АС, порядок астатизма.
2. Повторить основные разделы «Теории автоматического управления» (линейной):
· Динамические характеристики АС;
· Структурный анализ АС;
· Анализ устойчивости АС;
· Оценка точности АС.
В соответствии с номером варианта, привести решение заданий с первого по девятое.
3. Для заданной передаточной функции системы, в соответствии с номером варианта (задание 10), с помощью программного пакета Scilab (или SimInTech, Simulink,Vissim) найти и построить:
· переходную функцию системы;
· импульсно-переходную функцию;
· амплитудно-фазовую характеристику;
· логарифмическую амплитудно-частотную характеристику;
· логарифмическую фазовую частотную характеристику;
· полюса и нули передаточной функции и их графическое представление.
Сделать выводы об устойчивости заданной системы.
4. Отчет по практике. Отчет должен включать: титульный лист, задание, содержание, результаты выполнения каждого пункта задания.
| Задание на учебную практику (1-5) | |||||
| Вариант (номер по списку) | Найти производную функции h(t) | Найти передаточную функцию системы 𝑊 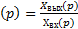 ) по известному дифференциальному уравнению. Начальные условия – нулевые. ) по известному дифференциальному уравнению. Начальные условия – нулевые.
| Найти первообразную функции w(t) | Записать преобразование Лапласа для функции w(t) | Определить аналитическое выражение для амплитудно-частотной характеристики 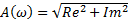 соответствующее функции соответствующее функции
|
| 1. | 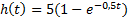
| 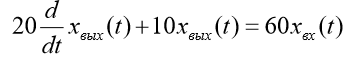
| 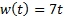
| 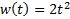
| 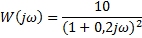
|
| 2. | 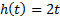
| 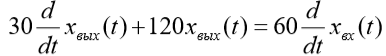
| 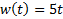
| 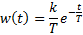
| 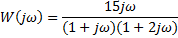
|
| 3. | 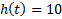
| 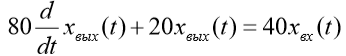
| 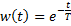
| 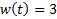
| 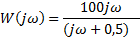
|
| 4. | 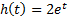
| 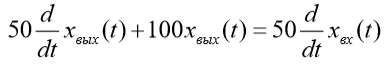
| 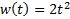
| 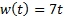
| 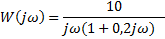
|
| 5. | 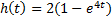
| 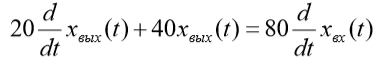
| 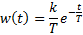
| 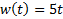
| 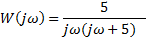
|
| 6. | 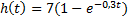
| 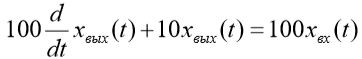
| 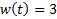
| 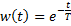
| 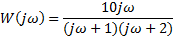
|
| 7. | 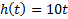
| 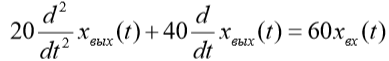
| 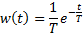
| 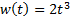
| 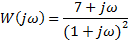
|
| 8. | 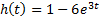
| 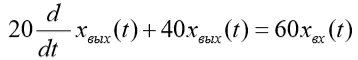
| 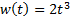
| 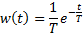
| 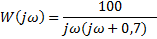
|
| 9. | 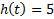
| 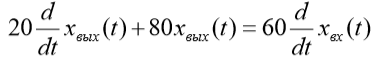
| 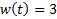
| 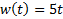
| 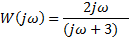
|
| 10. | 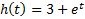
| 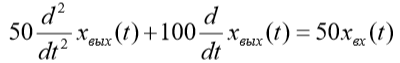
| 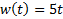
| 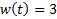
| 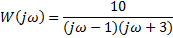
|
| 11. | 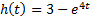
| 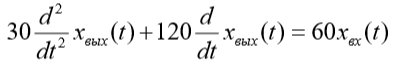
| 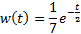
| 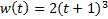
| 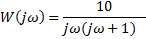
|
| 12. | 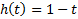
| 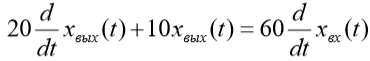
| 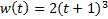
| 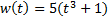
| 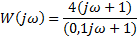
|
| 13. | 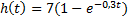
| 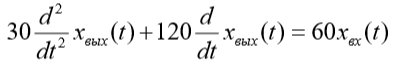
| 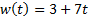
| 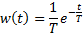
| 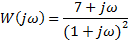
|
| 14. | 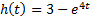
| 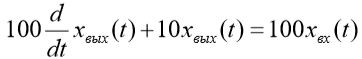
| 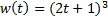
| 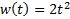
| 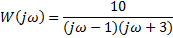
|
| 15. | 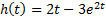
| 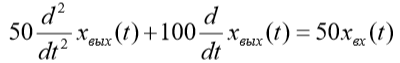
| 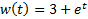
| 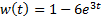
| 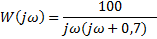
|
| Задание на учебную практику (6-8) | |||
| Вариант | Найти корни уравнения | Определить аналитическое выражение для фазовой частотной характеристики 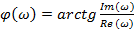 , соответствующее функции , соответствующее функции
| Решить дифференциальное уравнение |
| 1. | 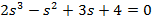
| 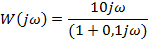
| 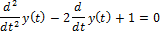
|
| 2. | 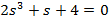
| 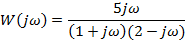
| 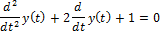
|
| 3. | 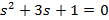
| 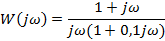
| 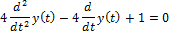
|
| 4. | 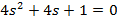
| 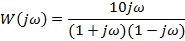
| 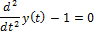
|
| 5. | 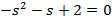
| 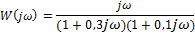
| 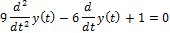
|
| 6. | 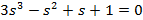
| 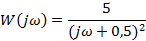
| 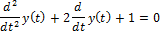
|
| 7. | 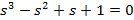
| 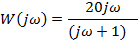
| 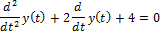
|
| 8. |
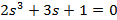
| 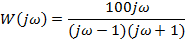
| 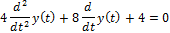
|
| 9. | 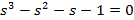
| 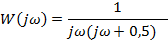
| 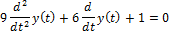
|
| 10. | 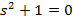
| 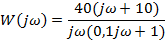
| 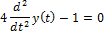
|
| 11. | 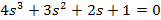
| 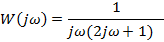
| 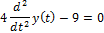
|
| 12. | 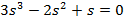
| 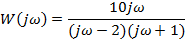
| 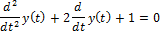
|
| 13. | 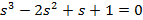
| 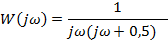
| 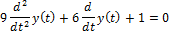
|
| 14. | 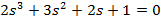
| 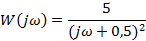
| 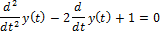
|
| 15. | 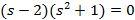
| 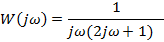
| 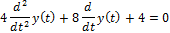
|
 2020-08-05
2020-08-05 103
103






