Решение показательных уравнений и неравенств.
Решение тригонометрических уравнений и неравенств.
Цели занятия:
Образовательная: Совершенствовать знания, умения, навыки по данной теме
Воспитательная: Формирование нравственных качеств
Развивающая: Развитие познавательной активности
Обеспечение занятия: доска, ручка, бумага, учебник
Задание№1. Решить уравнение 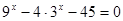 .
.
ü Заменой 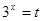 данное уравнение сводится к квадратному уравнению
данное уравнение сводится к квадратному уравнению 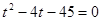 . Решая это уравнение, находим его корни:
. Решая это уравнение, находим его корни: 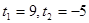 , откуда
, откуда  ,
, 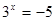 . Уравнение
. Уравнение  имеет корень
имеет корень 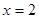 , а уравнение
, а уравнение 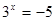 не имеет корней, так как показательная функция не может принимать отрицательные значения.
не имеет корней, так как показательная функция не может принимать отрицательные значения.
Задание№2. Решить уравнение  .
.
ü Так как 5>0, 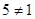 , то
, то  , откуда
, откуда 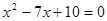 ,
, 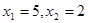 .
.
Задание№3. Решить неравенство  .
.
ü Заменой  ,тогда получим квадратное неравенство
,тогда получим квадратное неравенство 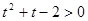 . Это неравенство выполняется при t <-2, и при t > 1.Так как
. Это неравенство выполняется при t <-2, и при t > 1.Так как  , то получим два неравенства
, то получим два неравенства  Первое неравенство не имеет решений, так как
Первое неравенство не имеет решений, так как 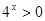 при всех
при всех  Второе неравенство можно записать в виде
Второе неравенство можно записать в виде 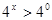 , откуда x > 0.
, откуда x > 0.
Задание№4. Решить уравнение  .
.
ü Вспомним, что cos x – это абсцисса точки окружности с радиусом, равным 1, полученной в результате поворота точки Р (1; 0) на угол х вокруг начала координат.
Абсцисса 1/2 есть у двух точек окружности 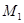 и
и 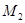 . Так как 1/2 = cos
. Так как 1/2 = cos 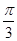 , то точку
, то точку 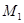 мы можем получить из точки Р (1; 0) путем поворота на угол
мы можем получить из точки Р (1; 0) путем поворота на угол 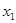 = π/3, а также на углы
= π/3, а также на углы
х = 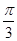 + 2πk, где k = +/-1, +/-2, …
+ 2πk, где k = +/-1, +/-2, …
Точка 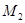 получается из точки Р (1; 0) поворотом на угол
получается из точки Р (1; 0) поворотом на угол 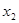 = -
= - 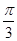 , а также на углы
, а также на углы
- 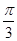 + 2πk, где k = +/-1, +/-2, …
+ 2πk, где k = +/-1, +/-2, …
Итак, все корни уравнения cos x = 1/2 можно найти по формулам х = 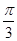 + 2πk
+ 2πk
х = - 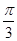 + 2πk, где k € Z.
+ 2πk, где k € Z.
Две представленные формулы можно объединить в одну:
х =  + 2πk, k € Z.
+ 2πk, k € Z.
Задание№5. Решить уравнение 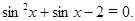
ü Это уравнение является квадратным относительно sin x. Обозначим sin x = y, получим уравнение  Его корни
Его корни 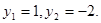 Таким образом, решение исходного уравнения свелось к решению простейших уравнений sin x =1 и sin x = -2.
Таким образом, решение исходного уравнения свелось к решению простейших уравнений sin x =1 и sin x = -2.
Уравнение sin x =1 имеет корни 
Уравнение sin x = -2 не имеет корней.
Задание№6. Решить уравнение sin7 x +sin3 x =3cos2 x.
ü Применяя формулу для суммы синусов, запишем уравнение в виде
2sin5 x cos2 x =3cos2 x,
2sin5 x cos2 x -3cos2 x =0, откуда 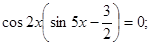
Уравнение 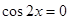 имеет корни
имеет корни 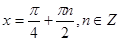 , а уравнение
, а уравнение 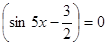 не имеет корней.
не имеет корней.
Упражнения
1.Решить уравнение:
1) 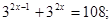 2)
2) 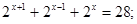
3) 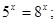 4)
4) 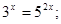
2. Решить уравнение:
1) 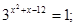 2)
2)  3)
3) 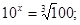 4)
4) 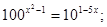
3. Решить уравнение:
1)  2)
2) 
3)  4)
4) 
4. Решить неравенство:
1) 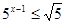 ; 2)
; 2)  ; 3)
; 3) 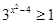 ; 4)
; 4) 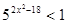 .
.
5. Решить неравенство:
1)  ; 2)
; 2) 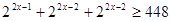 ;
;
3) 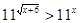 ; 4)
; 4)  .
.
6. Решить уравнение:
1)  ; 2)
; 2) 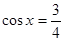 ; 3)
; 3) 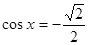 ; 4)
; 4) 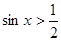 ; 5)
; 5) 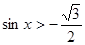 ; 6)
; 6)  ; 7)
; 7) 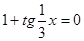 ; 8)
; 8) 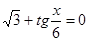 .
.
7. Решить уравнение:
1)  ; 2)
; 2) 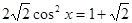 ;
;
8. Решить уравнение:
1) 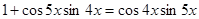 ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 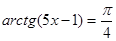 ;
;
5) 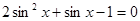 ; 6)
; 6) 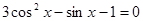 ;
;
7) 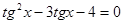 ; 8)
; 8)  ;
;
9)  ; 10)
; 10) 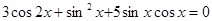 ;
;
11) 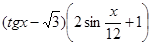 =0; 12)
=0; 12) 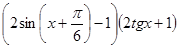 =0.
=0.
9. Найти все значения а, при которых уравнение 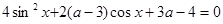 имеет корни, и решить это уравнение.
имеет корни, и решить это уравнение.
10.Решить неравенство:
1) 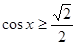 ; 2)
; 2)  ; 3)
; 3) 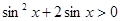 .
.
 2020-08-05
2020-08-05 54
54






