Дисциплина: ОДП.02 Математика
Группа: ТПОП -19
Дата: 09.06. 2020
Преподаватель: Кулага Т.Ф.
Задание: Ф ото выполненной работы прислать по адресу: kitdistergo@mail.ua kitdisttpop@mail.ua. или https://vk.com/id596417775 личным сообщением
(Название файла с ответами: № занятия, дисциплина, группа, Фамилия, имя, студента).
Например: Иванов И.И., ТПОП -19, Математика
Сроки выполнения: 10.06.2020
Задания для дистанционного обучения будут выдаваться в день проведения занятия, согласно расписанию и подмен по адресу: https://s3320.nubex.ru/5989/ или VK https://vk.com/ ТПОП-19, https://vk.com/ ТПОП-19
Мотивация
«Некоторую неудовлетворённость приносило только то, что для получения простого результата требовалось выполнение счётного множества условий.»
Гнеденко Б.В.
Тема занятия: Элементы комбинаторики. Комбинаторные задачи
Цели:
Обучающие:
- формирование основных понятий комбинаторики: размещения из mэлементов по n, сочетания из m элементов по n, перестановки из nэлементов;
- формирование умений и навыков вычисления значений комбинаторных выражений по формулам, решения простейших комбинаторных задач;
Развивающие:
-развитие умения анализировать, обобщать изучаемые факты, выделять и сравнивать существенные признаки, выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия; контроль и оценка процесса и результатов деятельности;
Воспитательные:
-воспитание интереса к дисциплине, честности, аккуратности, эстетического отношения к оформлению математических решений, воспитание умения слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, настойчивости в достижении цели и заинтересованности в конечном результате труда; прививать чувство патриотизма.
Посмотреть и прослушать видеоурок на сайтах Школа InternetUrok.ru, на Youtube по ссылке:
1. https://resh.edu.ru/subject/lesson/3993/main/225748/
2. https://www.youtube.com/watch?v=O3L5-x5wan4
Прочитать этот же материал по учебнику А. Алимов и др «Алгебра и начала математического анализа» 10-11 класс, 2016 г гл 11 §60.61
https://vpr-klass.com/uchebniki/matematika/10-11_klass_alimov/10-11_klass_alimov_uchebnik_chitat'_onlajn.html
Тема занятия: Элементы комбинаторики. Комбинаторные задачи
План: 1. Комбинаторика и ее возникновение. 2. Общие правила комбинаторики. 3. Генеральная совокупность без повторений и выборки без повторений. 4. Решении комбинаторных задач. 1. Комбинаторика и ее возникновение.   Комбинаторика- это область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих данному множеству. Комбинаторика возникла в XVI веке. В жизни привилегированных слоев тогдашнего общества большое место занимали азартные игры (карты, кости). Широко были распространены лотереи. Первоначально комбинаторные задачи касались в основном азартных игр: сколькими способами можно получить данное число очков, бросая 2 или 3 кости или сколькими способами можно получить 2-ух королей в некоторой карточной игре. Эти и другие проблемы азартных игр являлись движущей силой в развитии комбинаторики и далее в развитии теории вероятностей. Комбинаторика- это область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих данному множеству. Комбинаторика возникла в XVI веке. В жизни привилегированных слоев тогдашнего общества большое место занимали азартные игры (карты, кости). Широко были распространены лотереи. Первоначально комбинаторные задачи касались в основном азартных игр: сколькими способами можно получить данное число очков, бросая 2 или 3 кости или сколькими способами можно получить 2-ух королей в некоторой карточной игре. Эти и другие проблемы азартных игр являлись движущей силой в развитии комбинаторики и далее в развитии теории вероятностей.  Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья. Он составил таблицы (числа способов выпадения k очков на r костях). Однако, он не учел, одна и та же сумма очков может выпасть различными способами, поэтому его таблицы содержали большое количество ошибок. Теоретическое исследование вопросов комбинаторики предприняли в XVII веке французские математики Блез Паскаль и Ферма. Исходным пунктом их исследований были так же проблемы азартных игр. Дальнейшее развитие комбинаторики связано с именами Я. Бернулли, Г. Лейбница, Л. Эйлера. Однако, и в их работах основную роль играли приложения к различным играм. Сегодня комбинаторные методы используются для решения транспортных задач, в частности задач по составлению расписаний, для составления планов производства и реализации продукции и т.д. 2. Общие правила комбинаторики. Правило суммы:Если некоторый объект А может быть выбран m способами, а объект В- k способами, то объект «либо А, либо В» можно выбрать m+k способами. Примеры: 1. Допустим, что в ящике находится n разноцветных шаров. Произвольным образом вынимается 1 шарик. Сколькими способами это можно сделать? Ответ: n способами. Распределим эти n шариков по двум ящикам: в первый- m шариков, во второй- k шариков. Произвольным образом из произвольно выбранного ящика вынимается 1 шарик. Сколькими способами это можно сделать? Решение: Из первого ящика шарик можно вынуть m способами, из второго- k способами. Тогда всего способов m+k=n. 2.Морской семафор. В морском семафоре каждой букве алфавита соответствует определенное положение относительно тела сигнальщика двух флажков. Сколько таких сигналов может быть? Решение: Общее число складывается из положений, когда оба флажка расположены по разные стороны от тела сигнальщика и положений, когда они расположены по одну сторону от тела сигнальщика. При подсчете числа возможных положений применяется правило суммы. Правило произведения: Если объект А можно выбрать m способами, а после каждого такого выбора другой объект В можно выбрать (независимо от выбора объекта А) k способами, то пары объектов «А и В» можно выбрать m*k способами. Примеры: 1. Сколько двузначных чисел существует? Решение: Число десятков может быть обозначено любой цифрой от 1 до 9. Число единиц может быть обозначено любой цифрой от 0 до 9. Если число десятков равно 1, то число единиц может быть любым (от 0 до 9). Таким образом, существует 10 двузначных чисел, с числом десятков- 1. Аналогично рассуждаем и для любого другого числа десятков. Тогда можно посчитать, что существует 9 *10 = 90 двузначных чисел. 2. Имеется 2 ящика. В одном лежит m разноцветных кубиков, а в другом- k разноцветных шариков. Сколькими способами можно выбрать пару «Кубик-шарик»? Решение: Выбор шарика не зависит от выбора кубика, и наоборот. Поэтому, число способов, которыми можно выбрать данную пару равно m*k. 3. Генеральная совокупность без повторений и выборки без повторений. Генеральная совокупность без повторений- это набор некоторого конечного числа различных элементов a1, a2, a3,..., an. Пример:Набор из n разноцветных лоскутков. Выборкой объема k (k n)называется группа из m элементов данной генеральной совокупности. Пример:Пестрая лента, сшитая из m разноцветных лоскутков, выбранных из данных n. Размещениями из n элементов по kназываются такие выборки, которые содержат по k элементов, выбранных из числа данных n элементов генеральной совокупности без повторений, и отличаются друг от друга либо составом элементов, либо порядком их расположения. Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья. Он составил таблицы (числа способов выпадения k очков на r костях). Однако, он не учел, одна и та же сумма очков может выпасть различными способами, поэтому его таблицы содержали большое количество ошибок. Теоретическое исследование вопросов комбинаторики предприняли в XVII веке французские математики Блез Паскаль и Ферма. Исходным пунктом их исследований были так же проблемы азартных игр. Дальнейшее развитие комбинаторики связано с именами Я. Бернулли, Г. Лейбница, Л. Эйлера. Однако, и в их работах основную роль играли приложения к различным играм. Сегодня комбинаторные методы используются для решения транспортных задач, в частности задач по составлению расписаний, для составления планов производства и реализации продукции и т.д. 2. Общие правила комбинаторики. Правило суммы:Если некоторый объект А может быть выбран m способами, а объект В- k способами, то объект «либо А, либо В» можно выбрать m+k способами. Примеры: 1. Допустим, что в ящике находится n разноцветных шаров. Произвольным образом вынимается 1 шарик. Сколькими способами это можно сделать? Ответ: n способами. Распределим эти n шариков по двум ящикам: в первый- m шариков, во второй- k шариков. Произвольным образом из произвольно выбранного ящика вынимается 1 шарик. Сколькими способами это можно сделать? Решение: Из первого ящика шарик можно вынуть m способами, из второго- k способами. Тогда всего способов m+k=n. 2.Морской семафор. В морском семафоре каждой букве алфавита соответствует определенное положение относительно тела сигнальщика двух флажков. Сколько таких сигналов может быть? Решение: Общее число складывается из положений, когда оба флажка расположены по разные стороны от тела сигнальщика и положений, когда они расположены по одну сторону от тела сигнальщика. При подсчете числа возможных положений применяется правило суммы. Правило произведения: Если объект А можно выбрать m способами, а после каждого такого выбора другой объект В можно выбрать (независимо от выбора объекта А) k способами, то пары объектов «А и В» можно выбрать m*k способами. Примеры: 1. Сколько двузначных чисел существует? Решение: Число десятков может быть обозначено любой цифрой от 1 до 9. Число единиц может быть обозначено любой цифрой от 0 до 9. Если число десятков равно 1, то число единиц может быть любым (от 0 до 9). Таким образом, существует 10 двузначных чисел, с числом десятков- 1. Аналогично рассуждаем и для любого другого числа десятков. Тогда можно посчитать, что существует 9 *10 = 90 двузначных чисел. 2. Имеется 2 ящика. В одном лежит m разноцветных кубиков, а в другом- k разноцветных шариков. Сколькими способами можно выбрать пару «Кубик-шарик»? Решение: Выбор шарика не зависит от выбора кубика, и наоборот. Поэтому, число способов, которыми можно выбрать данную пару равно m*k. 3. Генеральная совокупность без повторений и выборки без повторений. Генеральная совокупность без повторений- это набор некоторого конечного числа различных элементов a1, a2, a3,..., an. Пример:Набор из n разноцветных лоскутков. Выборкой объема k (k n)называется группа из m элементов данной генеральной совокупности. Пример:Пестрая лента, сшитая из m разноцветных лоскутков, выбранных из данных n. Размещениями из n элементов по kназываются такие выборки, которые содержат по k элементов, выбранных из числа данных n элементов генеральной совокупности без повторений, и отличаются друг от друга либо составом элементов, либо порядком их расположения.  Формула для числа размещений. Размещениями из n элементов по m (мест) называются такие выборки, которые имея по m элементов, выбранных из числа данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения. Число размещений из n по m обозначается Anm и определяется по формуле Anm = n·(n − 1)·(n − 2)·...·(n − m + 1) = n!/(n − m)! Число размещений из n по k можно определить следующим способом: первый объект выборки можно выбрать n способами, далее второй объект можно выбрать n-1 способом и т.д. Формула для числа размещений. Размещениями из n элементов по m (мест) называются такие выборки, которые имея по m элементов, выбранных из числа данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения. Число размещений из n по m обозначается Anm и определяется по формуле Anm = n·(n − 1)·(n − 2)·...·(n − m + 1) = n!/(n − m)! Число размещений из n по k можно определить следующим способом: первый объект выборки можно выбрать n способами, далее второй объект можно выбрать n-1 способом и т.д. 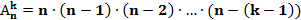 Преобразовав данную формулу, имеем: Преобразовав данную формулу, имеем: 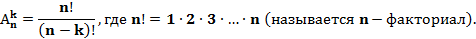 Следует помнить, что 0! =1. Примеры: 1. В первой группе класса А первенства по футболу участвует 17 команд. Разыгрываются медали: золото, серебро и бронза. Сколькими способами они могут быть разыграны? Решение:Комбинации команд-победителей отличаются друг от друга составом и порядком следования элементов, т.е. являются размещениями из 17 по 3. Следует помнить, что 0! =1. Примеры: 1. В первой группе класса А первенства по футболу участвует 17 команд. Разыгрываются медали: золото, серебро и бронза. Сколькими способами они могут быть разыграны? Решение:Комбинации команд-победителей отличаются друг от друга составом и порядком следования элементов, т.е. являются размещениями из 17 по 3. 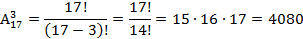 2. Научное общество состоит из 25-ти человек. Необходимо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами это можно сделать? Решение:Комбинации руководящего состава общества отличаются друг от друга составом и порядком следования элементов, т.е. являются размещениями из 25 по 4. 2. Научное общество состоит из 25-ти человек. Необходимо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами это можно сделать? Решение:Комбинации руководящего состава общества отличаются друг от друга составом и порядком следования элементов, т.е. являются размещениями из 25 по 4. 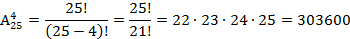  Перестановками без повторений из n элементовназываются размещения без повторений из n элементов по n, т.е. размещения отличаются друг от друга только порядком следования элементов. Формула для числа перестановок. Перестановками называются такие выборки элементов, которые отличаются только порядком расположения элементов, но не самими элементами. Если перестановки производятся на множестве из n элементов, их число определяется по формуле Pn = n·(n−1)·(n−2)...3·2·1 = n! n! - обозначение, которое используют для краткой записи произведения всех натуральных чисел от 1 до n включительно и называют "n-факториал" (в переводе с английского "factor" - "множитель"). Перестановками без повторений из n элементовназываются размещения без повторений из n элементов по n, т.е. размещения отличаются друг от друга только порядком следования элементов. Формула для числа перестановок. Перестановками называются такие выборки элементов, которые отличаются только порядком расположения элементов, но не самими элементами. Если перестановки производятся на множестве из n элементов, их число определяется по формуле Pn = n·(n−1)·(n−2)...3·2·1 = n! n! - обозначение, которое используют для краткой записи произведения всех натуральных чисел от 1 до n включительно и называют "n-факториал" (в переводе с английского "factor" - "множитель"). 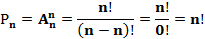 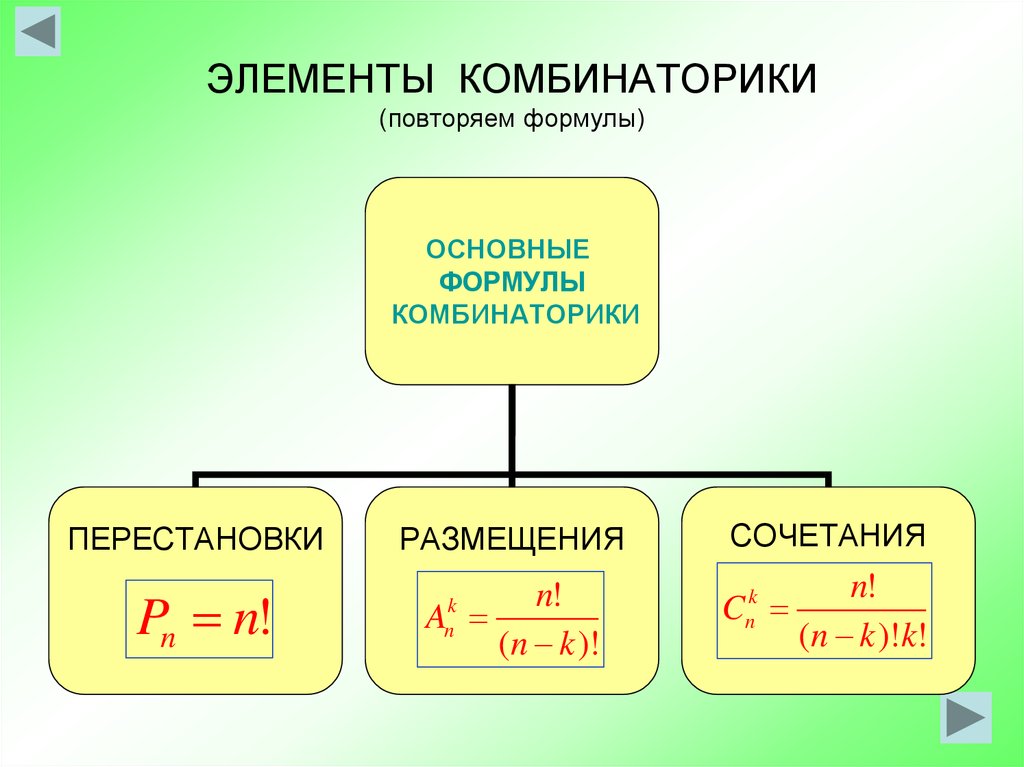 Задача 1. На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом 1-й и 2-й тома не стояли рядом? Решение. Определим общее число перестановок из 30 элементов по формуле P30 =30! Чтобы вычислить число "лишних" перестановок, сначала определим, сколько вариантов, в которых 2-й том находится рядом с 1-ым справа от него. В таких перестановках 1-ый том может занимать места с первого по 29-е, а 2-й со второго по 30-е - всего 29 мест для этой пары книг. И при каждом таком положении первых двух томов остальные 28 книг могут занимать остальные 28 мест в произвольном порядке. Вариантов перестановки 28 книг P28 =28! Всего "лишних" вариантов при расположении 2-го тома справа от 1-го получится 29·28! = 29!. Аналогично рассмотрим случай, когда 2-й том расположен рядом с 1-ым, но слева от него. Получается такое же число вариантов 29·28! = 29!. Значит всего "лишних" перестановок 2·29!, а нужных способов расстановки 30!−2·29! Вычислим это значение. 30! = 29!·30; 30!−2·29! = 29!·(30−2) = 29!·28. Итак, нам нужно перемножить все натуральные числа от 1 до 29 и еще раз умножить на 28. Ответ: 2,4757335·1032. Задача 2. На книжной полке стояло 30 томов. Ребенок уронил книги с полки, а затем расставил их в случайном порядке. Какова вероятность того, что он не поставил 1-й и 2-й тома рядом? Решение. Сначала определим вероятность события А, состоящего в том, что ребенок поставил 1-й и 2-й тома рядом. Элементарное событие - некая расстановка книг на полке. Понятно, что общее число всех элементарных событий будет равно общему числу всех возможных перестановок P30=30!. Число элементарных событий, благоприятствующих событию А, равно числу перестановок, в которых 1-й и 2-й тома стоят рядом. Мы рассматривали такие перестановки, решая предыдущую задачу, и получили 2·29! перестановок. Вероятность определяем делением числа благоприятствующих элементарных событий на число всех возможных элементарных событий: P(A) = 2·29!/30! = 2·29!/(29!·30) = 2/30 = 1/15. Событие В - ребенок не поставил 1-й и 2-й тома рядом - противоположно событию A, значит его вероятность P(B) = 1 − P(A) = 1−1/15 = 14/15 = 0,9333 Ответ: 0,9333. Примеры: 1. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что они должны состоять из различных цифр? Решение:Имеем перестановки из 5 элементов. Задача 1. На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом 1-й и 2-й тома не стояли рядом? Решение. Определим общее число перестановок из 30 элементов по формуле P30 =30! Чтобы вычислить число "лишних" перестановок, сначала определим, сколько вариантов, в которых 2-й том находится рядом с 1-ым справа от него. В таких перестановках 1-ый том может занимать места с первого по 29-е, а 2-й со второго по 30-е - всего 29 мест для этой пары книг. И при каждом таком положении первых двух томов остальные 28 книг могут занимать остальные 28 мест в произвольном порядке. Вариантов перестановки 28 книг P28 =28! Всего "лишних" вариантов при расположении 2-го тома справа от 1-го получится 29·28! = 29!. Аналогично рассмотрим случай, когда 2-й том расположен рядом с 1-ым, но слева от него. Получается такое же число вариантов 29·28! = 29!. Значит всего "лишних" перестановок 2·29!, а нужных способов расстановки 30!−2·29! Вычислим это значение. 30! = 29!·30; 30!−2·29! = 29!·(30−2) = 29!·28. Итак, нам нужно перемножить все натуральные числа от 1 до 29 и еще раз умножить на 28. Ответ: 2,4757335·1032. Задача 2. На книжной полке стояло 30 томов. Ребенок уронил книги с полки, а затем расставил их в случайном порядке. Какова вероятность того, что он не поставил 1-й и 2-й тома рядом? Решение. Сначала определим вероятность события А, состоящего в том, что ребенок поставил 1-й и 2-й тома рядом. Элементарное событие - некая расстановка книг на полке. Понятно, что общее число всех элементарных событий будет равно общему числу всех возможных перестановок P30=30!. Число элементарных событий, благоприятствующих событию А, равно числу перестановок, в которых 1-й и 2-й тома стоят рядом. Мы рассматривали такие перестановки, решая предыдущую задачу, и получили 2·29! перестановок. Вероятность определяем делением числа благоприятствующих элементарных событий на число всех возможных элементарных событий: P(A) = 2·29!/30! = 2·29!/(29!·30) = 2/30 = 1/15. Событие В - ребенок не поставил 1-й и 2-й тома рядом - противоположно событию A, значит его вероятность P(B) = 1 − P(A) = 1−1/15 = 14/15 = 0,9333 Ответ: 0,9333. Примеры: 1. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что они должны состоять из различных цифр? Решение:Имеем перестановки из 5 элементов. 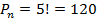 2. Сколькими способами можно собрать 6 разноцветных лоскутков в пеструю ленту? Решение:Имеем перестановки из 6 элементов. 2. Сколькими способами можно собрать 6 разноцветных лоскутков в пеструю ленту? Решение:Имеем перестановки из 6 элементов. 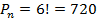 Сочетаниями без повторений из n элементов по kназываются такие выборки, которые содержат по k элементов, выбранных из числа данных n элементов генеральной совокупности без повторений, и отличаются друг от друга только составом элементов. Сочетаниями без повторений из n элементов по kназываются такие выборки, которые содержат по k элементов, выбранных из числа данных n элементов генеральной совокупности без повторений, и отличаются друг от друга только составом элементов. 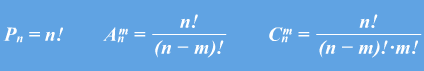 Примеры: 1. Если в полуфинале первенства по шахматам участвует 20 человек, а в финал выходят лишь трое, то сколькими способам и можно определить эту тройку? Решение:В данном случае порядок, в котором располагается эта тройка, не существенен. Поэтому тройки, вышедшие в финал, являются сочетаниями из 20 по 3. Примеры: 1. Если в полуфинале первенства по шахматам участвует 20 человек, а в финал выходят лишь трое, то сколькими способам и можно определить эту тройку? Решение:В данном случае порядок, в котором располагается эта тройка, не существенен. Поэтому тройки, вышедшие в финал, являются сочетаниями из 20 по 3. 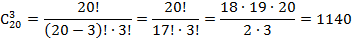 2. Сколькими способами можно выбрать трех делегатов из десяти человек на конференцию? Решение: В данном случае порядок, в котором располагается эта тройка, не существенен. Поэтому тройки делегатов являются сочетаниями из 10 по 3. 2. Сколькими способами можно выбрать трех делегатов из десяти человек на конференцию? Решение: В данном случае порядок, в котором располагается эта тройка, не существенен. Поэтому тройки делегатов являются сочетаниями из 10 по 3. 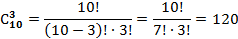   |
Домашнее задание
 составить конспект
составить конспект
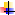 Решить №№1043 (1, 2), 1044 (1,2), 1053
Решить №№1043 (1, 2), 1044 (1,2), 1053
 фото прислать на электронную почту техникума kitdisttpop@mail.ua kitdisttpop@mail.ua. или VK https://vk.com/feed с полным названием ФИО студента, группа (например - Иванов И.И., ТПОП-19, Математика)
фото прислать на электронную почту техникума kitdisttpop@mail.ua kitdisttpop@mail.ua. или VK https://vk.com/feed с полным названием ФИО студента, группа (например - Иванов И.И., ТПОП-19, Математика)
Срок выполнения до 10.06.20
КРИТЕРИИ ОЦЕНИВАНИЯ
Ответ оценивается отметкой «5», если:
· работа выполнена полностью;
· в логических рассуждениях и обосновании решения нет пробелов и ошибок;
· в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
· работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
· допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
· допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но учащийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
· допущены существенные ошибки, показавшие, что учащийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится в случае:
· полного незнания изученного материала, отсутствия элементарных умений и навыков.
 2020-08-05
2020-08-05 1064
1064






