2020-08-05
73
ИТОГОВАЯ Контрольная работа по математике за II семестр.
Цели: Проверить знания, умения и навыки по Разделам 7,9. Определить уровень усвоения знаний, оценить результат деятельности студентов.
Ход работы:
Решить и правильно оформить задачи из трёх разделов математики по вариантам!
Определить свой вариант (см. таблицу ниже!). Решить контрольную работу.
Для того, чтобы работа была зачтена, нужно решить не менее 2-х задач на выбор из каждого раздела (I, II, III)
Вариант
I. Даны векторы 
(3;4;0); 
(1;-1;2).
а) Найти сумму векторов и ?
в) Найти координаты вектора 
коллинеарного вектору ?
с) Найти угол между векторами и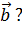 
II.1) Найти производную у = х4– х3 + ctg x + 2
2). Найти наибольшее и наименьшее значение функции f(x)= 2х3– 9x2 + 2 на отр. [1;3]
3). Материальная точка движется прямолинейно по закону х(t)= 2t3 +4t - 1
Найдите её скорость в момент времени t = 2с. (в метрах в секунду)
4).Исследовать функцию по схеме и построить график функции: у = x2 + 3
III а) Найти хотя бы одну первообразную функции у= 2t3 +4t – сos t
b) Вычислить интеграл по формуле Ньютона-Лейбница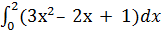 
c) Найти площадь фигуры, ограниченной линиями: у=х2, у=0; х=3.
Вариант
I. Даны векторы (- 3;0;4); (2;-1;1).
а) Найти сумму векторов и ?
в) Найти координаты вектора коллинеарного вектору ?
с) Найти угол между векторами и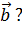
II.1) Найти производную у = 2х5– х2 + tg x + 1
2). Найти наибольшее и наименьшее значение функции f(x)= х4 -8х2-9 на отрезке [0;3]
3). Тело движется по закону S= 5х4- х2 +2х – 3. Определите скорость тела в конце 3й секунды
4).Исследовать функцию по схеме и построить график функции: у = 3x2 + 2
III а) Найти хотя бы одну первообразную функции у= t4 +t – sin t
b) Вычислить интеграл по формуле Ньютона-Лейбница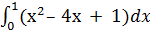 
c) Найти площадь фигуры, ограниченной линиями: у=4-х2, у=0.
Вариант
I. Даны векторы (4;0;3); (-2;1;5).
а) Найти сумму векторов и ?
в) Найти координаты вектора коллинеарного вектору ?
с) Найти угол между векторами и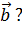
II.1) Найти производную у = х3– 2х2 + cos x + 12
2). Найти наибольшее и наименьшее значение функции f(x)= х3–3x2+3 на отрезке [1;3]
3). Материальная точка движется прямолинейно по закону х(t)= t4 +2t - π
Найдите её скорость в момент времени t = 2с. (в метрах в секунду)
4).Исследовать функцию по схеме и построить график функции: у = x2 + 3
III а) Найти хотя бы одну первообразную функции у= 3t3 +2t – et
b) Вычислить интеграл по формуле Ньютона-Лейбница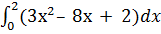 
c) Найти площадь фигуры, ограниченной линиями: у=2x-х2, у=0.
Вариант
I. Даны векторы (0;3;4); (- 1;2;1).
а) Найти сумму векторов и ?
в) Найти координаты вектора коллинеарного вектору ?
с) Найти угол между векторами и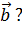
II.1) Найти производную у = х5– 3х2 + ln x + 5
2). Найти наибольшее значение функции f(x)=ln х–x на интервале(0;3)
3). Материальная точка движется прямолинейно по закону х(t)= 2t2 +4t - 7
Найдите её скорость в момент времени t = 2с. (в метрах в секунду)
4).Исследовать функцию по схеме и построить график функции: у = x2 – 4x+5
III а) Найти хотя бы одну первообразную функции у = 4t3 +2t – 1/ t
b) Вычислить интеграл по формуле Ньютона-Лейбница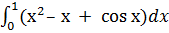 
c) Найти площадь фигуры, ограниченной линиями: у=х2-4x+5 у=0; х=0; x=4.
Вариант
I. Даны векторы (- 4;0;3); (5;2;1).
а) Найти сумму векторов и ?
в) Найти координаты вектора коллинеарного вектору ?
с) Найти угол между векторами и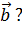
II.1) Найти производную у = х5– 2х3 + sin x + 1
2). Найти наибольшее значение функции f(x)= х3 -3х2 на отрезке [2;5]
3). Тело движется по закону S= х3- х2 +х – 2. Определите скорость тела в конце 2й секунды
4).Исследовать функцию по схеме и построить график функции: у = -x2 -4x
III а) Найти хотя бы одну первообразную функции у= x4 +2x –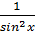 
b) Вычислить интеграл по формуле Ньютона-Лейбница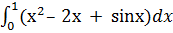 
c) Найти площадь фигуры, ограниченной линиями: у=-х2 -4х, у=0; х=-3; х=-1.
Вариант
I. Даны векторы (0;-4;3); (3;1;2).
а) Найти сумму векторов и ?
в) Найти координаты вектора коллинеарного вектору ?
с) Найти угол между векторами и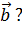
II.1) Найти производную у = х3– 2х2 + ex + 2
2). Найти наибольшее значение функции f(x)=6 cos х - 3х на отрезке [0;π/2]
3). Материальная точка движется прямолинейно по закону х(t)= 2t4 +2t - 3
Найдите её скорость в момент времени t = 3с. (в метрах в секунду)
4).Исследовать функцию по схеме и построить график функции: у = x2 – 2x+4
III а) Найти хотя бы одну первообразную функции у= 2x3 +x – ax
b) Вычислить интеграл по формуле Ньютона-Лейбница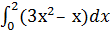 
c) Найти площадь фигуры, ограниченной линиями: у=х2-2х+4; у=3; х=-1.
Вариант
I. Даны векторы (3 ;0;-4); (6;-2;1).
а) Найти сумму векторов и ?
в) Найти координаты вектора коллинеарного вектору ?
с) Найти угол между векторами и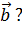
II.1) Найти производную у = х7– х5 + ax + 11
2). Найти наибольшее значение функции f(x)= 8x-х3 на отрезке [-3;1]
3). Тело движется по закону S= х2 - х – 2. Определите скорость тела в конце 5й секунды
4).Исследовать функцию по схеме и построить график функции: у = x2 +4x
III а) Найти хотя бы одну первообразную функции у= x2 + x +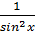
b) Вычислить интеграл по формуле Ньютона-Лейбница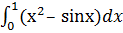 
c) Найти площадь фигуры, ограниченной линиями: у=х2 , у=0; х=1; х=2.
Вариант
I. Даны векторы (4;-3;0); (2;4;1).
а) Найти сумму векторов и ?
в) Найти координаты вектора коллинеарного вектору ?
с) Найти угол между векторами и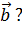
II.1) Найти производную у = х10– 2х4 + ex + 22
2). Найти наименьшее значение функции f(x)= -х3 +3х+7 на отрезке [-3;3]
3). Материальная точка движется прямолинейно по закону х(t)= 2t5 +2t - 13
Найдите её скорость в момент времени t = 2с. (в метрах в секунду)
4).Исследовать функцию по схеме и построить график функции: у = x2 + 4x+4
III а) Найти хотя бы одну первообразную функции у= 8x3 +6x – ax
b) Вычислить интеграл по формуле Ньютона-Лейбница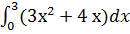 
c) Найти площадь фигуры, ограниченной линиями: у=х2+4х+4; у=0; х=0.
ТАБЛИЦА ДЛЯ ОПРЕДЕЛЕНИЯ ВАРИАНТА ВЫПОЛНЕНИЯ К.Р.№9
| вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| № по журналу | 1, 9, 17, 25 | 2, 10, 18,26 | 3, 11, 19,27 | 4, 12, 20,28 | 5, 13, 21,29 | 6, 14, 22,30 | 7. 15, 23,31 | 8, 16, 24,32 |
