2020-08-05
108
Последовательное соединение проводников
Последовательным называют такое соединение, при котором конец одного проводника соединяется с началом другого (рис. 1).
R1 R2 R3
 |
I1 I2 I3
Рис.1
При последовательном соединении проводников:
1. Сила тока во всех последовательно соединённых проводниках одинакова:
.
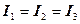2. Напряжение на концах участка цепи равно сумме напряжений на каждом проводнике:
.
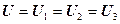3. Сопротивление участка цепи равно сумме сопротивлений отдельных проводников:
.
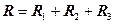Параллельное соединение проводников
Параллельным называют соединение, при котором концы всех проводников соединяются в один узел, а начала в другой (рис. 2). Для всех узлов сумма токов, входящих в узел, равна сумме токов, выходящих из узла, следовательно, I = I1 + I2 + I3+ …
R1 I1
|
|
|
 | |||
 | |||
I a R2 I2 b
R3 I3
 |
Рис. 2
Формула расчёта эквивалентного сопротивления n соединённых параллельно одинаковых резисторов выглядит следующим образом:
.
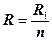Если параллельно соединено два различных сопротивления, то формула для расчёта имеет вид:
.
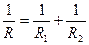
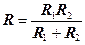Закон Ома для полной цепи
Полная замкнутая цепь представляет собой электрическую цепь, в состав которой входят внешнее сопротивление R и источник тока (рис. 3).
R
 |
I
r
- +
Рис. 3
Функция источника тока состоит в том, чтобы в процессе прохождения тока поддерживать постоянную разность потенциалов Δφ на своих полюсах. Под действием разности потенциалов по резистору R будет идти постоянный ток.
Энергетической характеристикой источника тока является электродвижущая сила (ЭДС) Е.
.
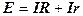Произведение силы тока на сопротивление участка цепи часто называют падением напряжения на этом участке. Таким образом, ЭДС равна сумме падений напряжений на внутреннем и внешнем участках замкнутой цепи. Обычно это выражение записываю так:
|
|
|
.
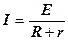Эту зависимость опытным путём получил Г. Ом, и называется она законом Ома для полной цепи и читается так: Сила тока в полной цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению цепи.
При разомкнутой цепи ЭДС равна напряжению на зажимах источника и, следовательно, может быть измерена вольтметром.
Законы Кирхгофа
Первый закон Кирхгофа является следствием закона сохранения количества электричества, согласно которому в узле заряд одного знака не может ни накапливаться, не убывать. Кроме того, первый закон Кирхгофа – это, по существу, закон сохранения энергии для электрических цепей. Его можно сформулировать следующим образом.
Сумма всех токов, приходящих к узлу электрической цепи, равна сумме всех токов, выходящих из этого узла. Иначе, алгебраическая сумма токов в узле равна нулю:
.
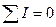Применительно к узлу, показанному на рис. 4, первый закон Кирхгофа можно записать так:
.
 |
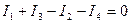I3 I4
 |
I2 I1
Рис. 4
Второй закон Кирхгофа применяют к замкнутым контурам. Он может быть сформулирован следующим образом:
Алгебраическая сумма напряжений на сопротивлениях участков замкнутого контура равна алгебраической сумме ЭДС источников, входящих в контур:
.
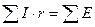Применительно к контуру, показанному на рис. 5, второй закон Кирхгофа можно записать так:
.
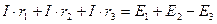I r1 E1 r2 E2 r3 E3
Рис. 5
