Примеры использования формул приведения

Формулы приведения, мнемоническое правило, доказательство, примеры.

Мы подробно разберем формулы приведения. Сначала мы дадим полный список формул приведения, и рассмотрим примеры их применения. Дальше остановимся на мнемоническом правиле, позволяющем легко получать формулы приведения без их запоминания. В заключение статьи покажем доказательство формул приведения.

Список формул приведения

Формулы приведения получили свое название не от слова «привиделось», а от слова «приводить». С их помощью синус, косинус, тангенс и котангенс произвольного угла можно привести к синусу, косинусу, тангенсу и котангенсу угла из интервала от 0 до 90 градусов (от нуля до пи пополам радиан). Таким образом, формулы приведения позволяют нам переходить к работе с углами в пределах 90 градусов, что, несомненно, очень удобно. В этом одна из их основных заслуг.

Прежде чем перечислить все формулы приведения отметим, что в этих формулах аргументами тригонометрических функций являются углы вида 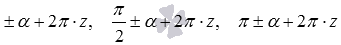и 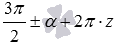, где z – любое целое число, а альфа – произвольный угол поворота.

И еще один момент: формул приведения достаточно много по количеству, и сразу предостережем Вас от заучивания их всех наизусть. В этом абсолютно нет необходимости – существует мнемоническое правило, позволяющее легко применять формулы приведения.

Итак, запишем все формулы приведения в виде таблицы.

Эти формулы можно переписать с использованием градусов и радиан. Для этого достаточно вспомнить про связь между градусами и радианами, и везде заменить π на 180 градусов.

Примеры использования формул приведения

Цель этого пункта заключается в том, чтобы показать, как формулы приведения используются на практике при решении примеров.

Для начала стоит сказать, что существует бесконечное число способов представления угла под знаком тригонометрических функций в виде 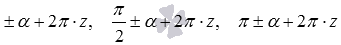и 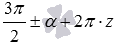. Это связано с тем, что угол может принимать любое значение. Покажем это на примере.

Для примера возьмем угол под знаком тригонометрической функции равным . Этот угол можно представить как , или как , или как , или еще множеством других способов.

А теперь давайте посмотрим, какие формулы приведения нам придется использовать в зависимости от представления угла. Для примера возьмем .

Если мы представим угол как , то этому представлению отвечает формула приведения вида , откуда получаем . Мы здесь можем указать значение тригонометрической функции: .

Для представления мы уже будем использовать формулу вида , которая нас приводит к следующему результату: .

Наконец, , так как соответствующая формула приведения имеет вид .

В заключение этих рассуждений стоит особо отметить, что существуют определенные удобства при использовании представлений угла, в которых угол 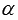имеет величину от 0 до 90 градусов (от 0 до пи пополам радиан).

Рассмотрим еще пример применения формул приведения.

Пример.

Используя формулы приведения, представьте через синус, а также через косинус острого угла.

Решение.

Чтобы применить формулы приведения, нам нужно угол 197 градусов представить в виде или , причем по условию задачи угол должен быть острым. Это можно сделать двумя способами: или . Таким образом, или .