Формулы приведения отражают периодичность, симметричность и свойства сдвига на углы 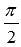 и
и  . Сразу заметим, что все формулы приведения можно доказывать, отбросив в аргументах слагаемое
. Сразу заметим, что все формулы приведения можно доказывать, отбросив в аргументах слагаемое  , так как оно означает изменение угла на целое число полных оборотов, а это не изменяет значения тригонометрических функций. Это слагаемое
, так как оно означает изменение угла на целое число полных оборотов, а это не изменяет значения тригонометрических функций. Это слагаемое  и служит отражением периодичности.
и служит отражением периодичности.
Первый блок из 16 формул приведения напрямую следует из свойств синуса, косинуса, тангенса и котангенса. На них даже не стоит останавливаться.
Переходим к следующему блоку формул. Сначала докажем первые две из них. Остальные следуют из них. Итак, докажем формулы приведения вида 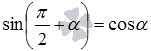 и
и  .
.
Рассмотрим единичную окружность. Пусть начальная точка A после поворота на угол 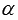 переходит в точку A1(x, y), а после поворота на угол
переходит в точку A1(x, y), а после поворота на угол 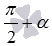 - в точку A2. Проведем A1H1 и A2H2 – перпендикуляры к прямой Ox.
- в точку A2. Проведем A1H1 и A2H2 – перпендикуляры к прямой Ox.
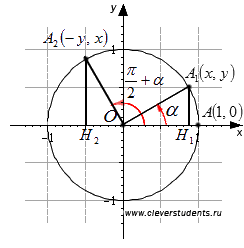
Несложно видеть, что прямоугольные треугольники OA1H1 и OA2H2 равны по гипотенузе и двум прилежащим к ней углам. Из равенства треугольников и расположения точек A1 и A2 на единичной окружности становится видно, что если точка A1 имеет координаты x и y, то точку A2 имеет координаты −y и x. Тогда определения синуса и косинуса позволяют нам записать равенства 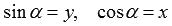 и
и 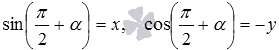 , откуда следует, что
, откуда следует, что 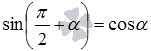 и
и  . Этим доказаны рассматриваемые формулы приведения для любого угла
. Этим доказаны рассматриваемые формулы приведения для любого угла 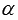 .
.
Учитывая, что  и
и 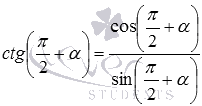 (при необходимости смотрите статью основные тригонометрические тождества), а также только что доказанные формулы, получаем
(при необходимости смотрите статью основные тригонометрические тождества), а также только что доказанные формулы, получаем 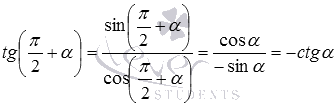 и
и 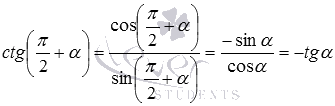 . Так мы доказали две следующие формулы приведения.
. Так мы доказали две следующие формулы приведения.
Для доказательства формул приведения с аргументом 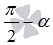 достаточно его представить как
достаточно его представить как 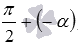 , после чего использовать доказанные формулы и свойства тригонометрических функций с противоположными аргументами. Например,.
, после чего использовать доказанные формулы и свойства тригонометрических функций с противоположными аргументами. Например,.
Аналогично доказываются и все остальные формулы приведения на базе уже доказанных путем двукратного применения. Например, 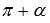 представляется как
представляется как 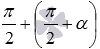 , а
, а  - как
- как 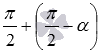 . А
. А 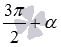 и
и 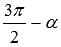 - как
- как 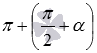 и
и 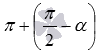 соответственно.
соответственно.
 2020-08-05
2020-08-05 291
291







