Лекция 15
60. Некоторые задачи на прямую и плоскость в пространстве
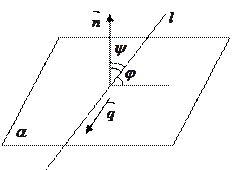 1). Найти угол между прямой и плоскостью.
1). Найти угол между прямой и плоскостью.
Углом между 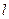 и
и 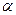 называется угол между
называется угол между 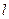 и ее проекцией на
и ее проекцией на 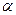 .
.
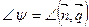 .
. 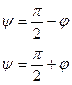
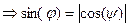 . Тогда
. Тогда
| (15.1) | 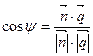 или или 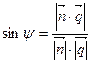 . .
|
 2). Написать уравнение перпендикуляра, опущенного из точки
2). Написать уравнение перпендикуляра, опущенного из точки 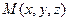 на прямую
на прямую 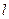 , заданную уравнением
, заданную уравнением 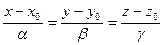 и найти расстояние от точки до прямой.
и найти расстояние от точки до прямой.
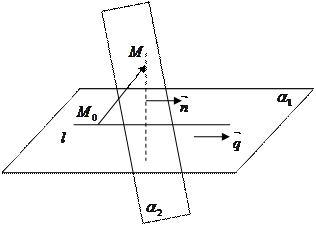
Построим плоскость 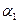 , содержащую точку
, содержащую точку 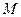 и прямую
и прямую 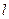 . Уравнение этой плоскости имеет вид:
. Уравнение этой плоскости имеет вид: 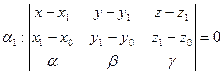 Построим также плоскость
Построим также плоскость 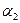 , проходящую через точку
, проходящую через точку 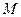 , перпендикулярно прямой
, перпендикулярно прямой 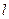 :
:
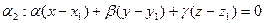 .
.
Система этих двух уравнений и дает искомый перпендикуляр.
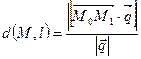 . (15.2)
. (15.2)
 3). Написать уравнение общего перпендикуляра к двум скрещивающимся прямым
3). Написать уравнение общего перпендикуляра к двум скрещивающимся прямым 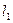 и
и 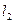 .
.
Пусть 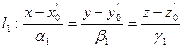 ,
, 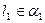 и
и 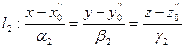 ,
, 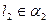 , тогда
, тогда 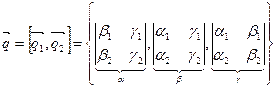 - является направляющим вектором искомого перпендикуляра.
- является направляющим вектором искомого перпендикуляра.
а) 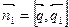 - вектор нормали плоскости
- вектор нормали плоскости 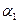 , которая содержит прямую
, которая содержит прямую 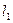 и
и 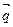 (или содержит искомый перпендикуляр).
(или содержит искомый перпендикуляр).
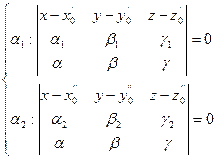 ,
,
Система этих двух уравнений задает искомый перпендикуляр.
Замечание: 1) 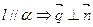 , т.е.
, т.е. 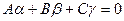 .
.
2) 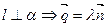 , т.е.
, т.е. 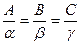 .
.
Поверхности II порядка
Алгебраическое уравнение II степени относительно 3-х переменных 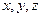 вида:
вида:
| (*) | 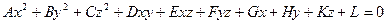 , ,
|
где 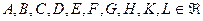 ,
, 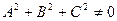 ,
,
определяет поверхность II порядка.
Будем изучать случаи, когда 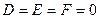 . Уравнение (*) при перечисленных условиях может определять сферу, эллипсоид, параболоид, цилиндрическую поверхность, коническую поверхность и гиперболоиды в зависимости от коэффициентов.
. Уравнение (*) при перечисленных условиях может определять сферу, эллипсоид, параболоид, цилиндрическую поверхность, коническую поверхность и гиперболоиды в зависимости от коэффициентов.
I тип задач
(по геометрическим свойствам поверхности определяется уравнение)
1) Сфера
Определение 15.1.
Множество точек пространства, равноудаленных от данной точки 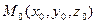 , называемой центром, называется сферой.
, называемой центром, называется сферой.
Выберем произвольную точку 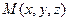 принадлежащую сфере, тогда
принадлежащую сфере, тогда 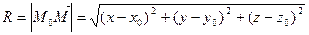 или
или
| (15.3) | 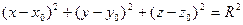
|
- каноническое уравнение сферы с центром 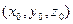 и радиусом
и радиусом 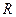 .
.
Цилиндрические поверхности
 Определение 15.2
Определение 15.2
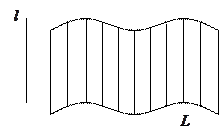
Цилиндрической поверхностью называется поверхность, описываемая прямой 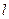 (образующей), движущейся вдоль некоторой линии
(образующей), движущейся вдоль некоторой линии 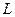 (направляющей) и остающейся параллельной исходному направлению.
(направляющей) и остающейся параллельной исходному направлению.
Если 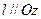 , то
, то 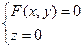 - определяет линию в плоскости
- определяет линию в плоскости 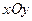 .
.
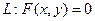 (не содержит переменной
(не содержит переменной 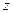 ).
).
Цилиндром II-го порядка называется цилиндрическая поверхность, направляющими которой являются эллипс, гипербола, парабола:
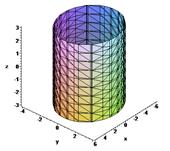
А) Эллиптический цилиндр.
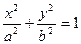
| 
|
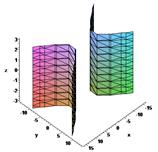
Б) Гиперболический цилиндр.
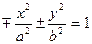
| 
|
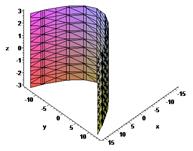
В) Параболический цилиндр.
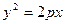
| 
|
 2020-08-05
2020-08-05 125
125







