2020-08-05
96
Определение 15.3
Поверхность, образованная прямыми, пересекающимися в одной точке и проходящими через каждую точку линии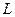 
- называется конической поверхностью.
| 
|
II тип задач
(по виду уравнения определяются свойства поверхности)
Основным методом решения таких задач является метод сечений, который заключается в поиске линий пересечений данной поверхности плоскостями, параллельными координатным плоскостям.
Эллипсоид
Определение 15.4.
Эллипсоидом называется поверхность, которая в прямоугольной системе координат определяется уравнением
. (15.4)
Установим геометрический вид эллипсоида.
Рассмотрим сечения эллипсоида плоскостями параллельными 
(
число).
Линия сечения определяется системой:
| (**) |  .
|
Исследуем (**).
А) 
, тогда 
- эллипс в плоскости 
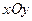, причем самый большой.
Б) 
, тогда 
- линия (**) вырождается в точки 
.
(плоскости 
касаются эллипсоида)
В) 
, тогда 
.
Таким образом, плоскость 
пересекает эллипсоид по эллипсу, причем, если 
, то 
, поэтому при 
, получается самый большой эллипс.
Г) 
, то 
- мнимый эллипс, точек пересечения с не 
.
- полуоси эллипсоида. Если 
, то эллипсоид является сферой.
Аналогично, если 
или 
.
Однополостной гиперболоид
Определение 15.5
Однополостным гиперболоидом называется поверхность, которая в прямоугольной системе координат определяется уравнением
. (15.5)
Установим его геометрический вид.
Рассмотрим сечения с координатными плоскостями:
и 
(В сечения получаются гиперболы)
Также рассмотрим сечения поверхности плоскостями :
.
А) , - самый маленький эллипс.
Б) 
, 
.
В) 
, 
, 
, то 
.
Г) 
, 
, то 
.
Таким образом, рассмотренные сечения позволяют изобразить однополостной гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления. 
- полуоси (чтобы изобразить 
, следует построить основной прямоугольник какой-нибудь из гипербол).
