2020-08-05
115
Пример 1.1
В однородном электрическом поле напряженностью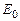 
закреплен точечный отрицательный заряд 
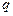. В точке A, положение которой определяется расстоянием 
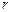и углом 
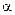(см. рис.), модуль вектора напряженности результирующего электрического поля 
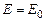. Определите угол 
.
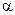Решениe.
Напряженность результирующего поля согласно принципу суперпозиции равна
,
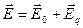где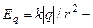 
напряженность поля, создаваемого точечным зарядом q в точке А (рис.)
|
.
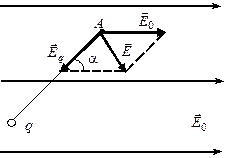
По теореме косинусов
.
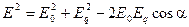Учитывая, что по условию задачи 
, получим для искомого угла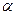 
:
.
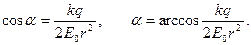Пример 1.2
Два одинаковых небольших металлических шарика с зарядам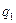и 
и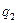 
, находящихся на расстоянии l = 0,2 м друг от друга притягиваются с силой 
H. После того как шарики привели в соприкосновение и опять развели на то же расстояние l, они стали отталкиваться с силой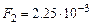 
Н. Найдите 
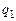и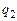 
.
Решение.
Так как в начале шарики притягивались, то их заряды противоположны по знаку и по закону Кулона
(1)
После того, как шарики были приведены в соприкосновение, заряды перераспределяются, и на каждом из шариков заряд, согласно закону сохранения заряда, становится равным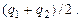 
Поэтому они стали взаимодействовать с силой
|
|
|
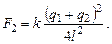(2)
Уравнения (1) и (2), дают систему уравнений для неизвестных 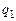и 
решив которую, находим искомые заряды
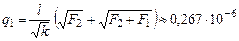Кл,
Кл.
Заметим, что в соответствии с симметрией задачи возможны и
такие значения зарядов: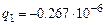 
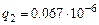Кл, 
Кл.
Пример 1.3
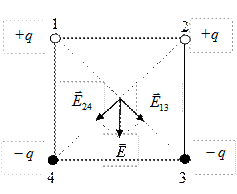
В вершинах квадрата, со стороной а, помещены четыре заряда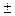 
q (см. рис.).
Найдите напряженность электрического поля на перпендикуляре, восстановленном из центра квадрата, как функцию его длины x.
Решение.
Из принципа суперпозиции полей, результирующее поле, создаваемое зарядами, равно:
 
| 
|
= 
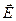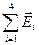, где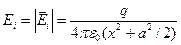 
.
Задача сводится к суммированию четырех равных по величине, но разных по направлению векторов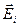 
. Найдем векторную сумму полей положительного и отрицательного зарядов 1 и 3. Из подобия треугольников на рисунке получим:
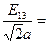
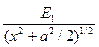, т.е. 
.
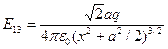Аналогично, складывая поля 2-го и 4-го зарядов найдем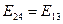 
. Для сложения векторов 
и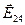 
учтем их равенство по величине и взаимную перпендикулярность. По теореме Пифагора, получим
.
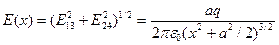Пример 1.4
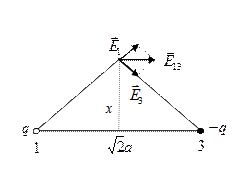
На рисунке изображена одна из линий напряженности электрического поля двух неподвижных точечных зарядов 
и 
. Известно, что 
нКл. Определите .
|
Решение.
Введем систему координат, выбрав ее, как показано на рисунке, т.е. ось x проходит через заряды, а ось y проходит через «вершину» линии поля. Так как вектор поля направлен по касательной к линии поля, то в точке «вершины» Еy = 0. По принципу суперпозиции для поля в этой точке имеем:
|
|
|
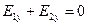, где
,
.
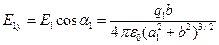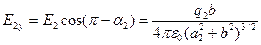После подстановки и преобразований, найдем, взяв значения геометрических параметров из рисунка в условии задачи a 1 =2, a 2 = 8, b = 4:
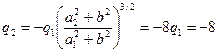нКл.
