| Номер вида | Уравнение поверхности | Название поверхности | Рисунок поверхности |
| 1 | 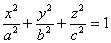
| Эллипс | 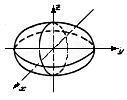
|
| 2 | 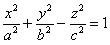
| Однополостный гиперболоид | 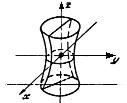
|
| 3 | 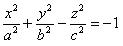
| Двуполостный гиперболоид | 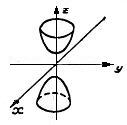
|
| 4 | 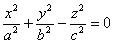
| Конус второго порядка | 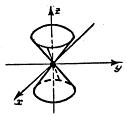
|
| 5 | 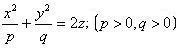
| Эллиптический параболоид | 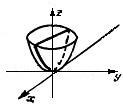
|
| 6 | 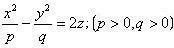
| Гиперболический параболоид | 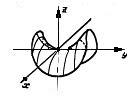
|
| 7 | 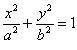
| Эллиптический цилиндр | 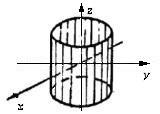
|
| 8 | 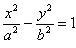
| Гиперболический цилиндр | 
|
| 9 | y 2 = px; (p > 0) | Параболический цилиндр | 
|
СОДЕРЖАНИЕ ТИПОВОГО РАСЧЕТА
Семь алгебраических поверхностей второго порядка заданы уравнениями вида
| Ax 2 + By 2 + Cz 2 + Dx + Ey + Fz + G = 0 | (8.9) |
Определить тип каждой поверхности и сделать рисунок.
ПРИМЕР ВЫПОЛНЕНИЯ ТИПОВОГО РАСЧЕТА
В условии заданы коэффициенты уравнения (8.9) в виде таблицы:
| N | A | B | C | D | E | F | G |
| 1 | 1 | –4 | –1 | 2 | –8 | 2 | 0 |
Приведем решение этой задачи. По условию уравнение имеет вид
x 2 – 4 y 2 – z 2 + 2 x – 8 y + 2 z = 0.
Выделим полные квадраты и приведем уравнение к виду:
(x 2 + 2 x + 1) – 1 – 4(y + 1)2 + 4 – (z – 1)2 + 1 = 0
(x + 1)2 – 4(y + 1)2 – (z – 1)2 = – 4

Положим x' = x + 1, y' = y + 1 и z' = z – 1. Это означает переход к новой ДПСК, которая получается из данной параллельным переносом и начало которой в т. O' (–1, –1, 1).
Теперь, наше уравнение примет вид:
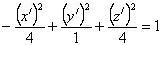 или или 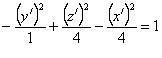
| (8.10) |
и мы можем определить тип поверхности – однополостный гиперболоид, “нанизанный” на ось абсцисс новой ДПСК, т.е. на прямую, параллельную оси OX и проходящую через т. O' (–1, –1, 1) (заметим, что уравнение (8.10) не является в строгом смысле каноническим уравнением однополостного гиперболоида; чтобы его получить, нужно “поменять” оси O' X' и O' Z', т.е. повернуть ДПСК O' X' Y' Z' вокруг оси O' Y' на 90° по часовой стрелке).
Сводка полученных результатов
| Данное уравнение поверхности | x 2 – 4 y 2 – z 2 + 2 x – 8 y +2 z = 0 |
| Уравнение поверхности относительно ДПСК O'X'Y' (после параллельного переноса) | 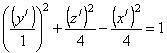
|
| Название поверхности | Однополостный гиперболоид |
| Связь между координатами Точки (X, Y, Z) и (X', Y', Z') |  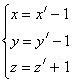
|
| Координаты центра O' | (–1, –1, 1) |
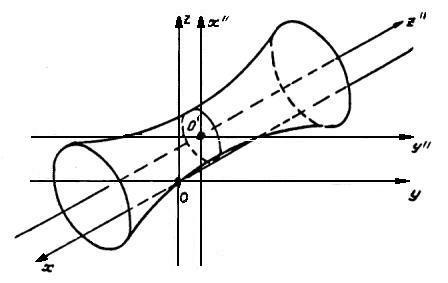
Однополостный гиперболоид
Рис. 8.1
Оформление отчета
Все результаты каждой задачи должны быть сведаны в таблицу, как это сделано в примере. Таблица должна содержать данные уравнение поверхности, каноническое уравнение и название поверхности: формулы, связывающие координаты точки относительно рассматриваемых ДПСК, координаты начала новой ДПСК в данной ДПСК.
Должен быть сделан аккуратный рисунок поверхности в данной ДПСК.
Работа должна содержать не только ответы на вопросы, поставленные в задании, но и все вычисления, на основании которых сделаны выводы.
 2020-08-05
2020-08-05 130
130







