Рассмотрим решение задач на нахождение площади поверхностей и объема пирамиды

 

Задача 1

Основанием пирамиды является квадрат ABCD со стороной 4 см, высота – отрезок .

Найти площадь боковой поверхности пирамиды.

Решение.

1. Из условия следует, что МА⊥АВС.

Прямоугольные треугольники МАВ и MAD равны по двум катетам, отсюда . Треугольники МCD и МСВ равны по трем сторонам.

Отсюда следует: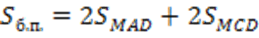

2. AD – проекция прямой MD на плоскость АВС, AD⊥DC⇒MD⊥DC,

отсюда имеем прямоугольный треугольник MDC.

3. В прямоугольном треугольнике MAD найдем по теореме Пифагора гипотенузу:

 

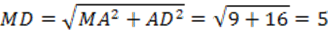
4. Найдем площадь рассматриваемого прямоугольного треугольника MAD:

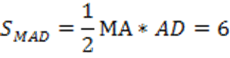
5. Рассмотрим прямоугольный треугольник MDC и найдем его площадь:

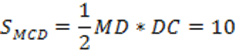
6. Так, площадь боковой поверхности пирамиды:

.

Ответ: 32 кв.см.

 

Задача 2

В правильной треугольной пирамиде сторона основания 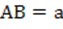, высота .

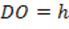Найти: апофему 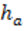,  боковое ребро l,

           площадь боковой поверхности S,

   тангенс угла наклона бокового ребра к плоскости основания,

    угол между АВ и CD.

Построить: общий перпендикуляр к прямым АВ и CD.

Решение:

Рис. к задаче 2

1. Правильная треугольная пирамида полностью задается двумя элементами, в данном случае:

- стороной основания a и высотой h.

2. Зная свойства правильного треугольника и зная выражение радиусов вписанной и описанной окружностей через высоту, определим, что в прямоугольных треугольниках  и DOC нам известны:

- их общий катет – высота пирамиды ,

- вторые катеты: .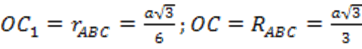

 

3. Можем найти гипотенузы по теореме Пифагора, при этом:

- гипотенуза  является искомой апофемой h_a,

- гипотенуза DС – боковым ребром пирамиды l.

   

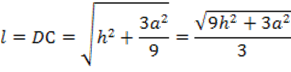
4. Вычислим боковую поверхность пирамиды:

 

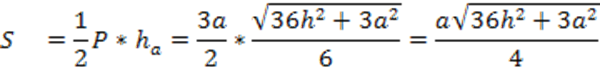
5. Напомним, что углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость.

Нам необходимо найти тангенс угла наклона бокового ребра к основанию пирамиды. То есть нам необходимо найти .

Напомним, что тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего ему катета к прилежащему. Получим:

 

7. Осталось найти угол между скрещивающимися прямыми АВ и CD.

Докажем, что этот угол равен .

СО есть проекция наклонной DC на плоскость АВС.

Но СО (или 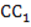) перпендикулярна АВ, отсюда DC⊥AB.

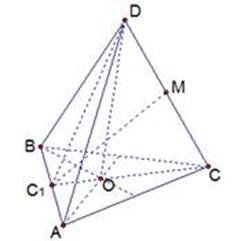Рис. К Построению

общего перпендикуляра к скрещивающимся прямым AD и CD

8. Построим общий перпендикуляр к двум скрещивающимся прямым АВ и CD (см.Рис.).

Очевидно, что точка  – середина ребра АВ.

Проведем  перпендикулярно DC.

Докажем, что :

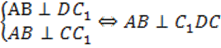
Так, общим перпендикуляром к рассматриваемым скрещивающимся прямым  АВ и CD является отрезок .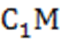

 

 

Итак, все задания в задаче выполнены.

 

 

Домашнее задание

Призма

(решение задач обязательно сопровождать схемой, на которую необходимо ссылаться в решении)

В заданиях 1-5 значение символа N – номер студента в классном журнале.

 

Задание № 1

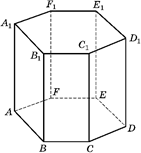
Найти площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна N ед., а высота – (N+2) ед.

 

Задание № 2

Площадь поверхности куба равна N кв.ед.

Найдите его диагональ.

 

Задание № 3

Если каждое ребро куба увеличить на 1, то его площадь поверхно­сти увеличится на N.

Найдите ребро куба.

Задание № 4

Во сколько раз увеличится объем куба, если его ребра увеличить в N раз?

 

Задание № 5

Объем одного куба в N раз больше объема другого куба.

Во сколько раз площадь поверхности первого куба больше площа­ди поверхности второго куба?

 

Пирамида

(решение задач обязательно сопровождать схемой, на которую необходимо ссылаться в решении)

В задачах 1-3 значение символа N – это номер студента в классном журнале.

Задача 1

Cтороны основания правильной четырехугольной пирамиды равны N, боковые ребра – 2N.

Найдите площадь поверхности пирамиды.

 

 

Задача 2

Основание пирамиды – прямоугольник. Одна боковая грань перпендикулярна основанию, остальные наклонены под углом . Высота пирамиды – (N+5) см.

Найдите площадь основания.

 

Задача 3

Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в N раз?

 

Примечание:

1. Дистанционный материал изучить, конспектируя в тетрадь по математике.

2. Материал по теме – выучить.

3. Рассмотреть и разобрать решение представленных типовых задач.

4. Выполнить домашнее задание в тетради по математике.

5. Качественные (резкие, не затемненные, расположенные в вертикально) фото/скан:

- конспект,

- решение типовых задач,

- домашнее задание, -

прислать на страницу преподавателя для проверки.

 

Материал по одной теме присылать отдельно от других тем. Страницы работы должны быть размещены последовательно (не в разброс!), и технически так, чтобы можно было «листать страницы», не открывая каждую страницу темы отдельно.