Способ прямоугольных координат (перпендикуляров) обычно применяют при наличии строительной сетки. В качестве исходных данных для разбивки точки этим способом используются прямоугольные координаты пунктов строительной сетки и точек сооружения.
Пусть требуется найти на местности положения точек С и D основной оси сооружения от пунктов 3 А 4 B и 3 А 5 В строительной сетки (рис. 1.20). Координаты точек С и D в системе строительной сетки соответственно
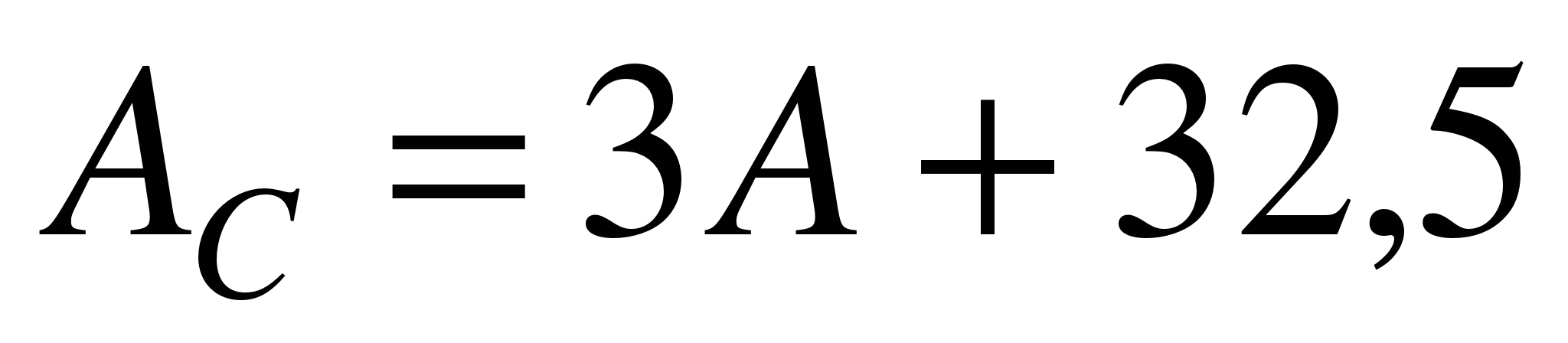 ,
, 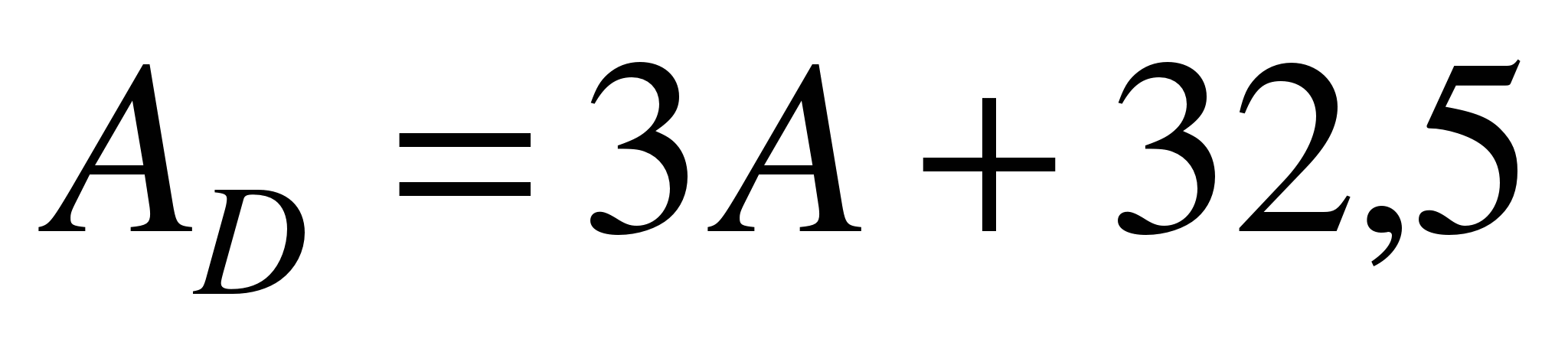 ;
;
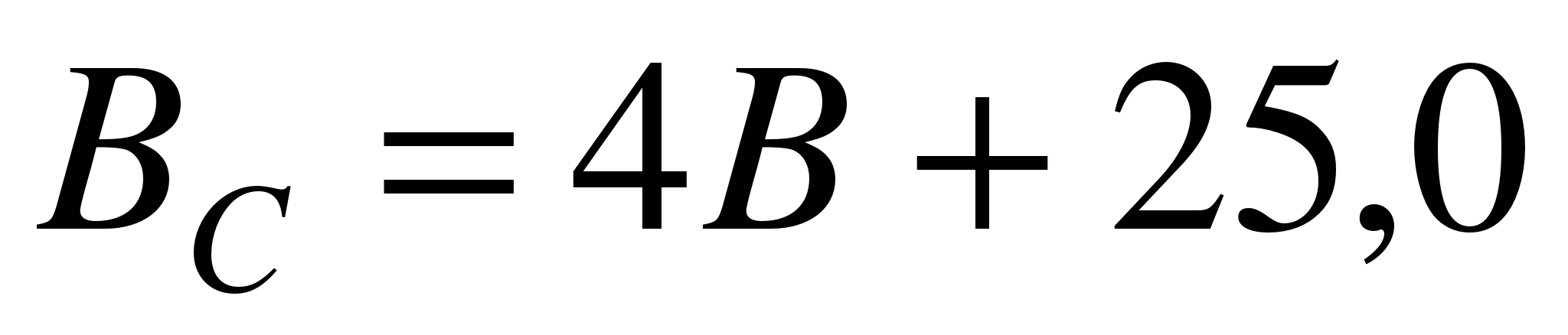 ,
, 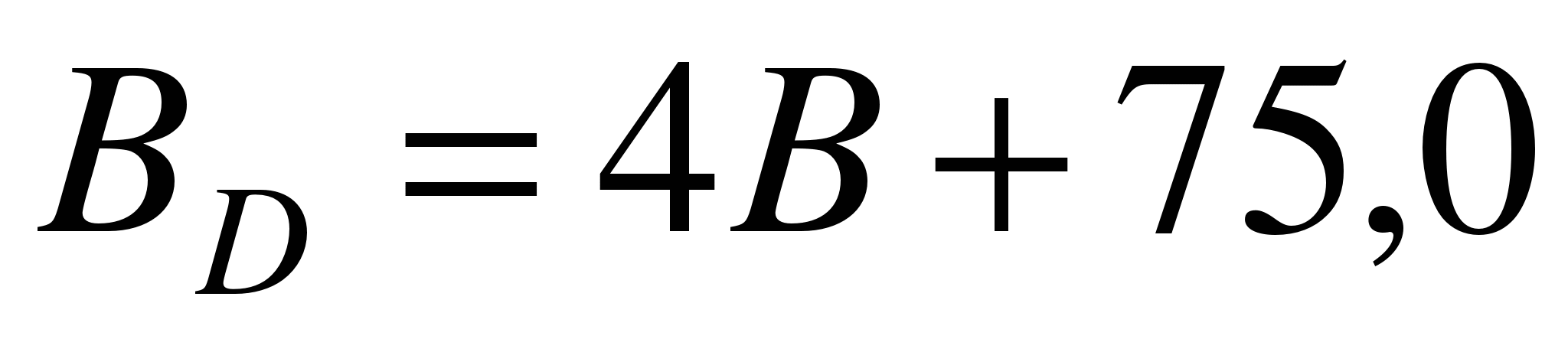 .
.
По координатам пунктов 3 А 4 B и 3 А 5 В и точек С и D вычисляют расстояния 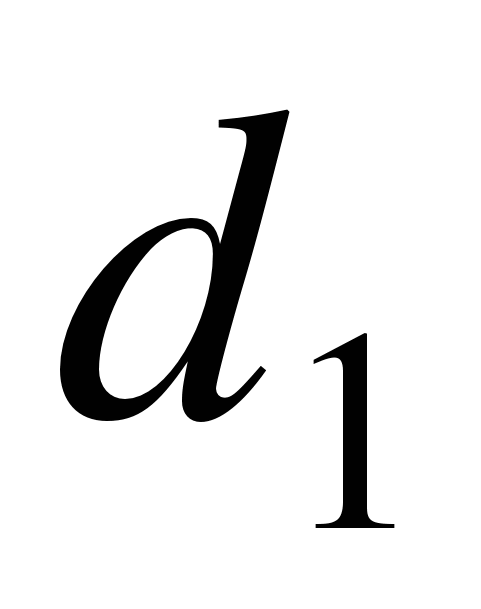 ,
, 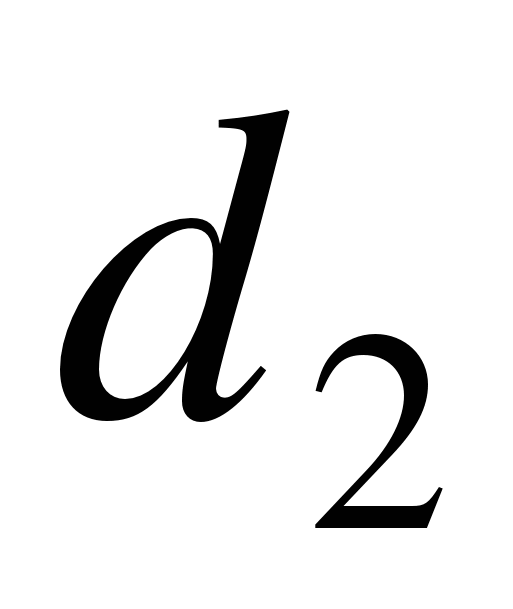 ,
, 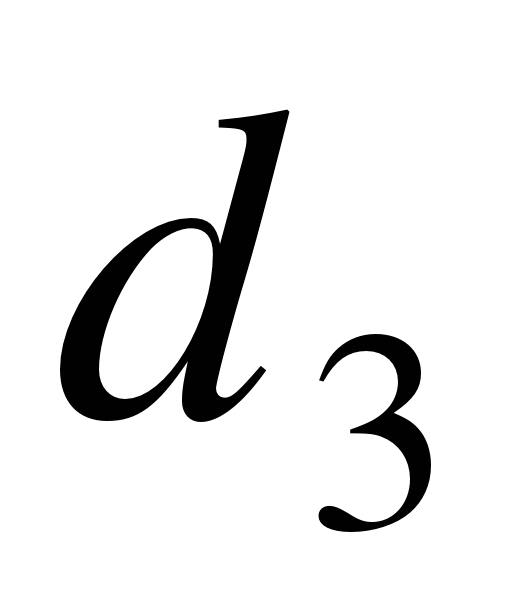 и
и  :
:
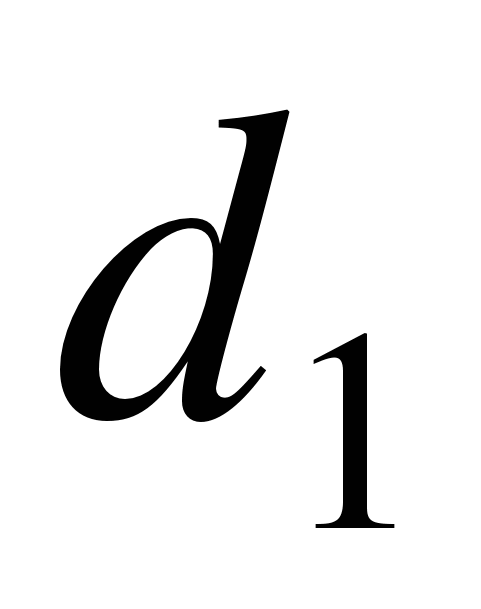 = 425,0 – 400,0 = 25,0 м;
= 425,0 – 400,0 = 25,0 м; 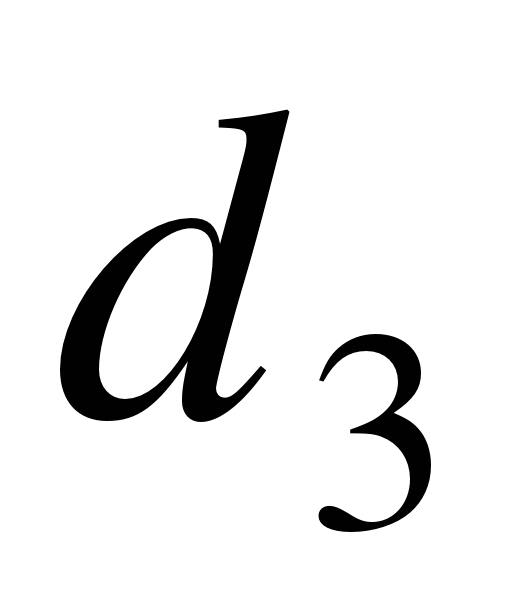 = 500,0 – 475,0 = 25,0 м;
= 500,0 – 475,0 = 25,0 м;
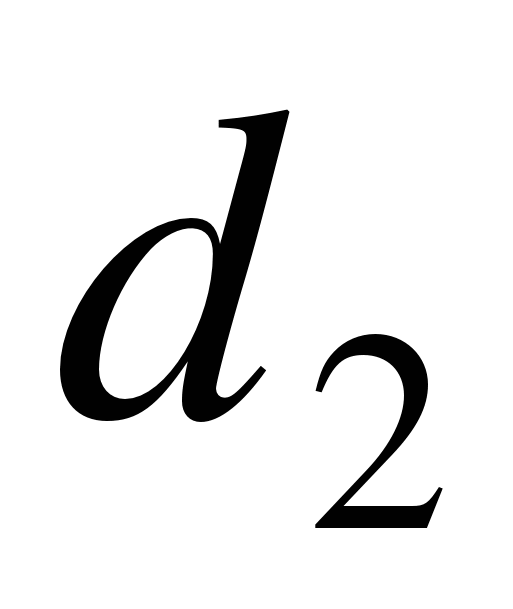 = 332,5 – 300,0 = 32,5 м;
= 332,5 – 300,0 = 32,5 м;  = 332,5 – 300,0 = 32,5 м.
= 332,5 – 300,0 = 32,5 м.
От пунктов 3 А 4 B и 3 А 5 В откладывают отрезки 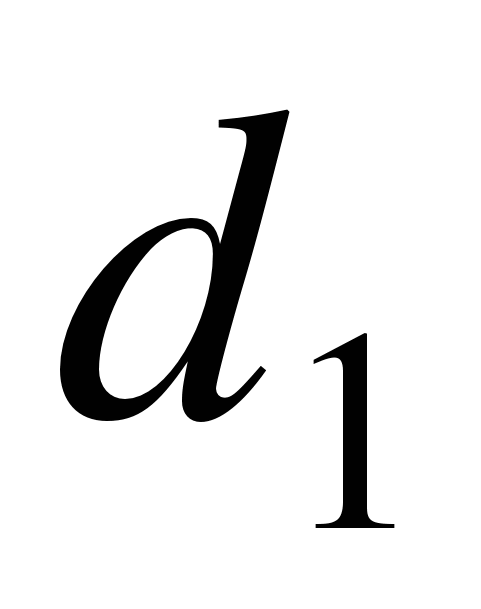 и
и 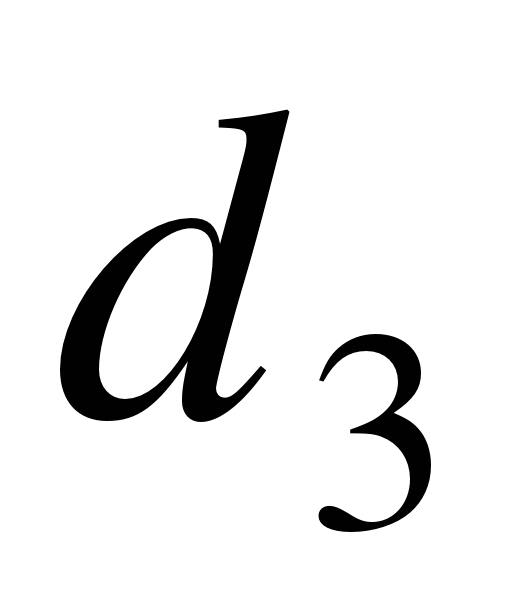 . В полученных точках с помощью теодолита строят прямые углы и по перпендикулярам откладывают отрезки
. В полученных точках с помощью теодолита строят прямые углы и по перпендикулярам откладывают отрезки 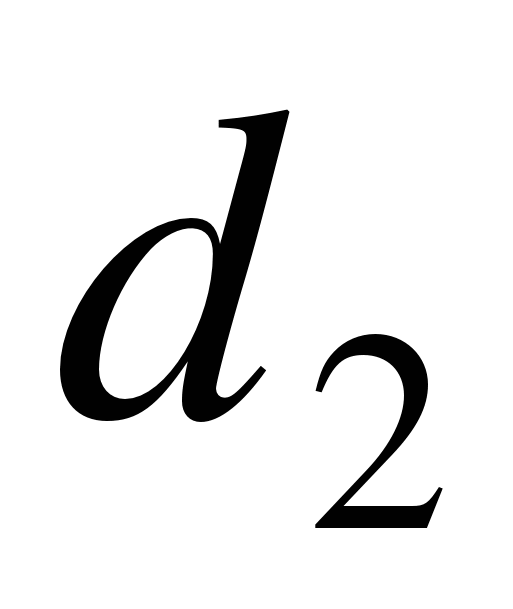 ,
,  . Точность отложения углов и линий выбирают по характеристике сооружения (см. табл. 1.2).
. Точность отложения углов и линий выбирают по характеристике сооружения (см. табл. 1.2).
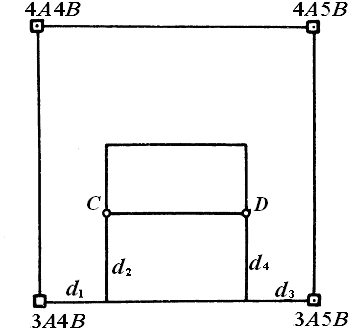
Рис. 1.20. Вынос точек способом перпендикуляров
При необходимости средняя квадратическая погрешность выноса на местность точки С может быть предвычислена по формуле
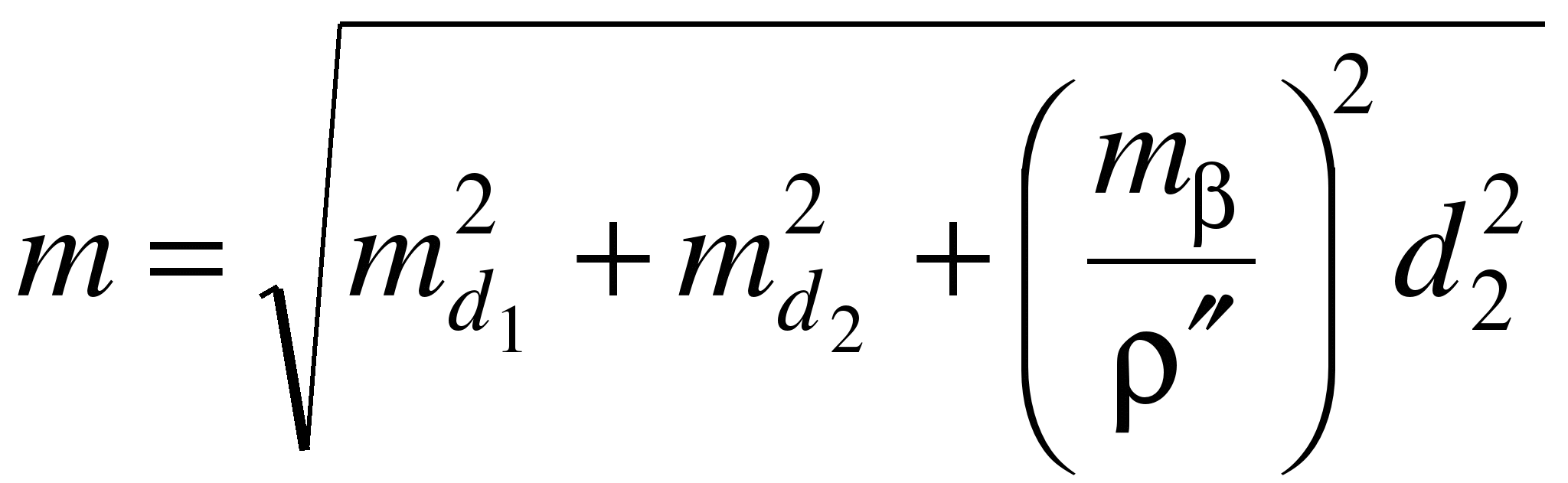 , (1.25)
, (1.25)
где 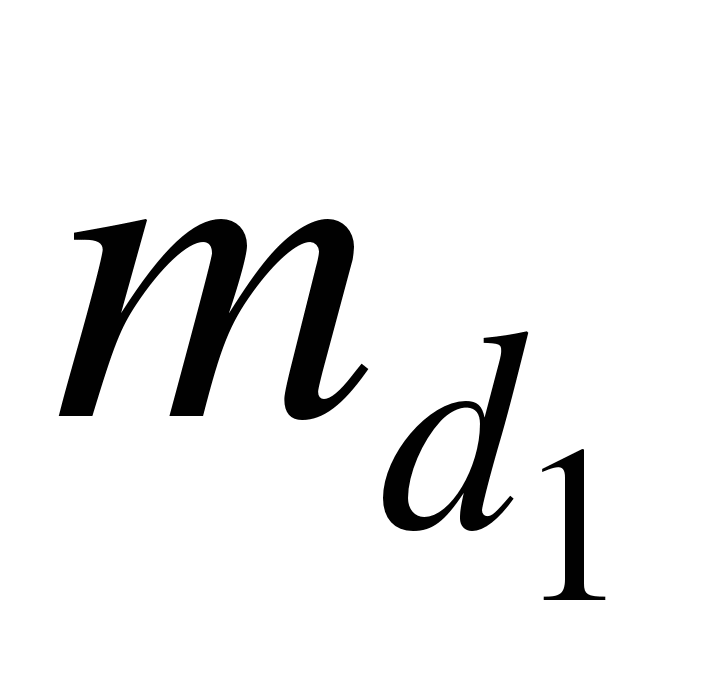 и
и 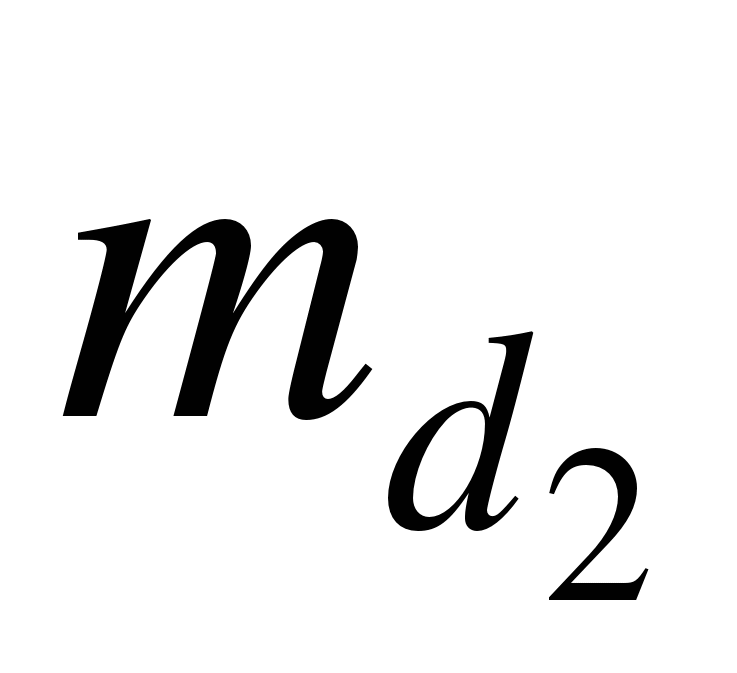 – средние квадратические погрешности отложения расстояний
– средние квадратические погрешности отложения расстояний 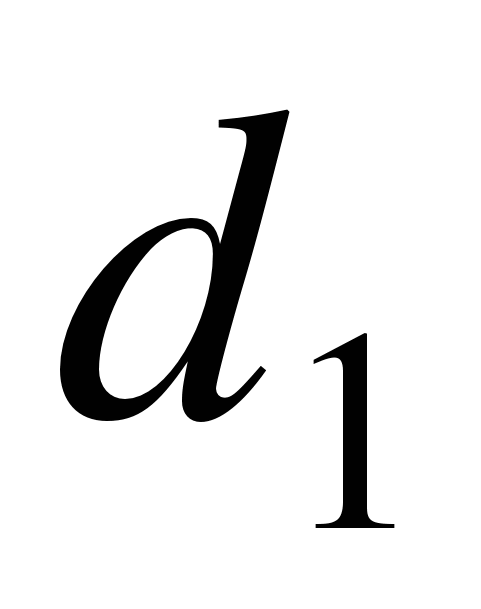 и
и 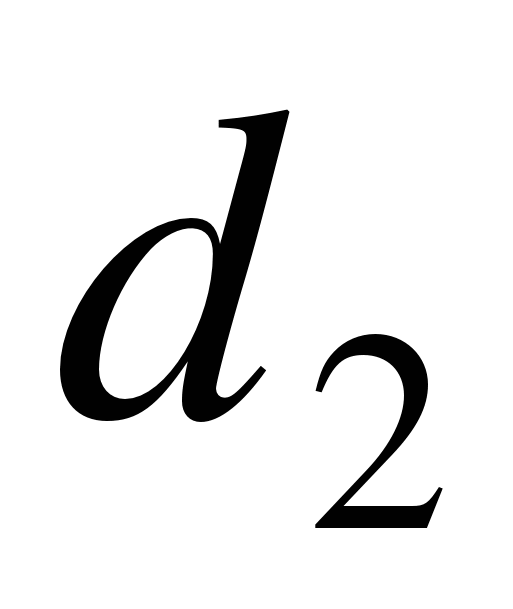 ;
; 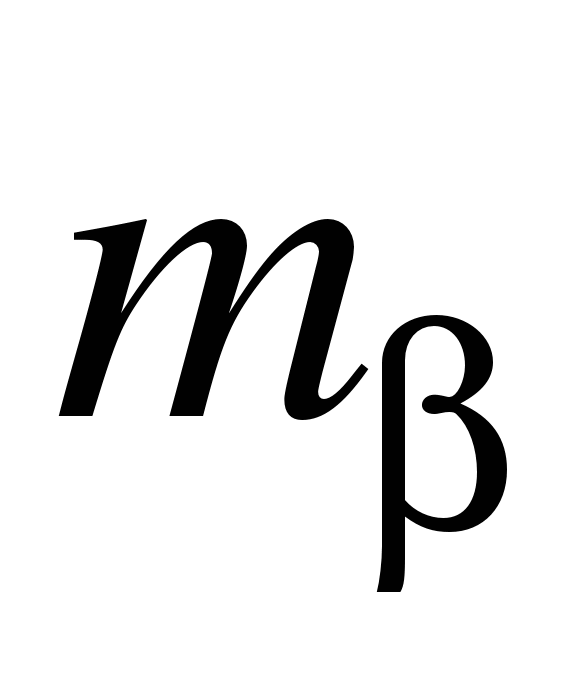 – средняя квадратическая погрешность построения прямого угла.
– средняя квадратическая погрешность построения прямого угла.
1.6.2. Способ прямой угловой засечки
На пересеченной местности линейные измерения и построения мерными лентами и рулетками затруднены или даже невозможны. В этом случае точки проекта рекомендуется выносить способом прямой угловой засечки, требующей построения на местности только двух горизонтальных углов. Преимущества способа проявляются и в том случае, когда расстояния до пунктов разбивочной сети велики.
|
|
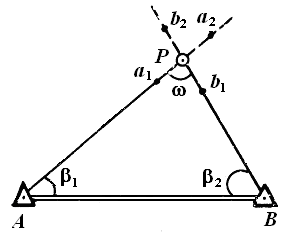
| Рис. 1.21. Построение точки способом прямой угловой засечки |
Между точками 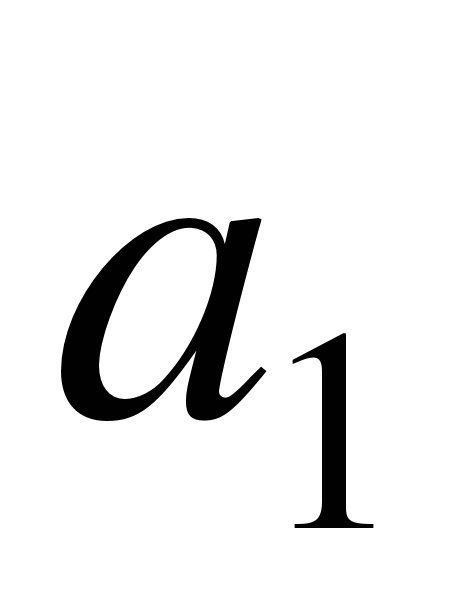 и
и 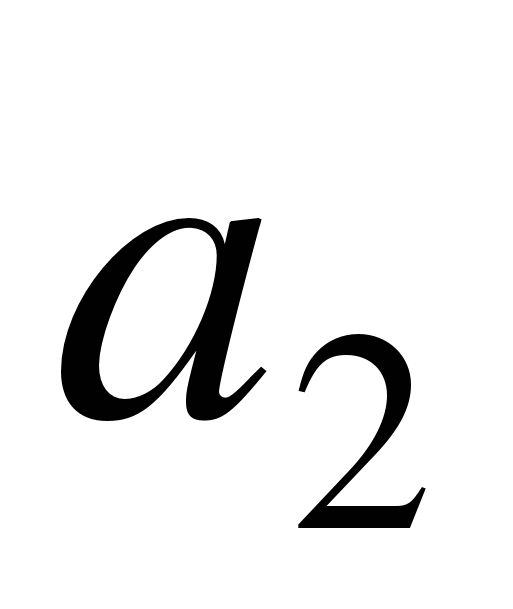 ,
, 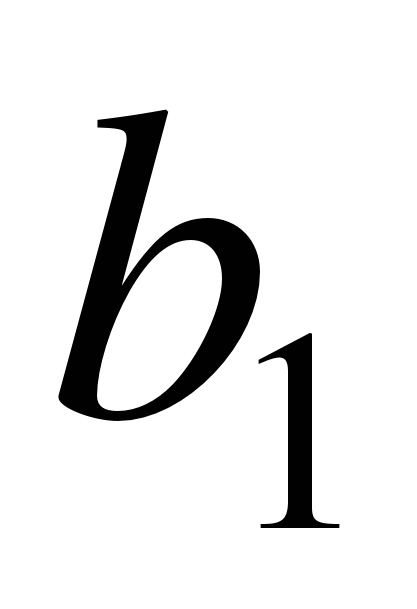 и
и 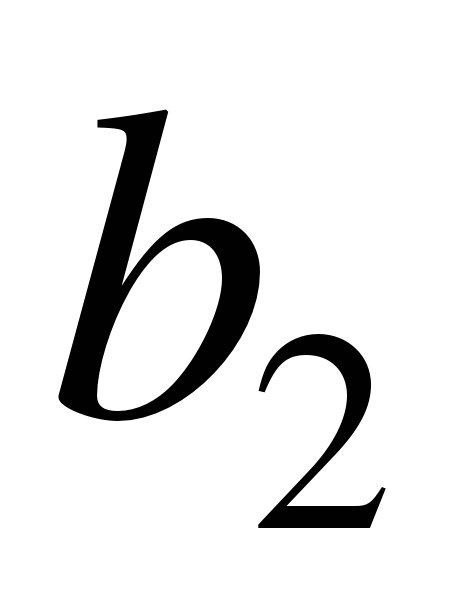 натягивают проволоки и в точке их пересечения находят положение выносимой точки Р. Угол засечки
натягивают проволоки и в точке их пересечения находят положение выносимой точки Р. Угол засечки  должен быть от 30 до 150°. Углы
должен быть от 30 до 150°. Углы 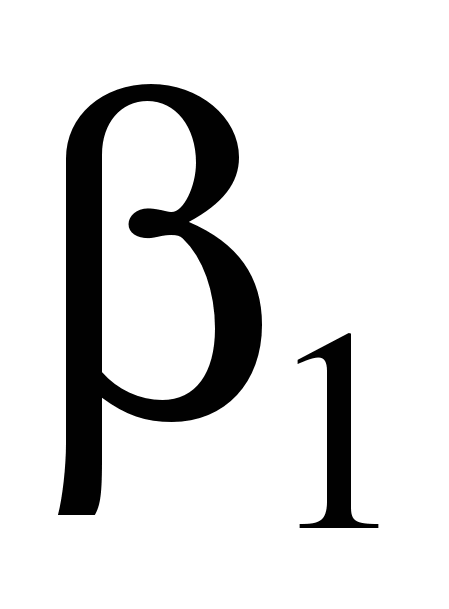 и
и 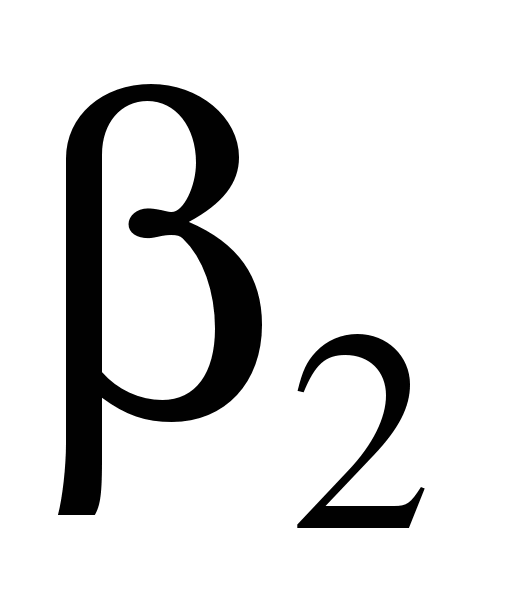 вычисляют с использованием формул обратной геодезической задачи:
вычисляют с использованием формул обратной геодезической задачи:
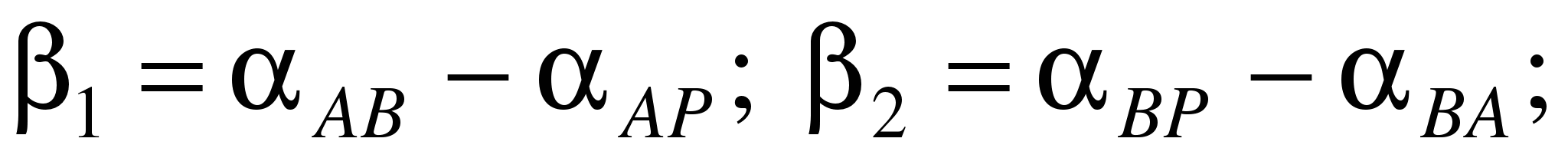 (1.26)
(1.26)
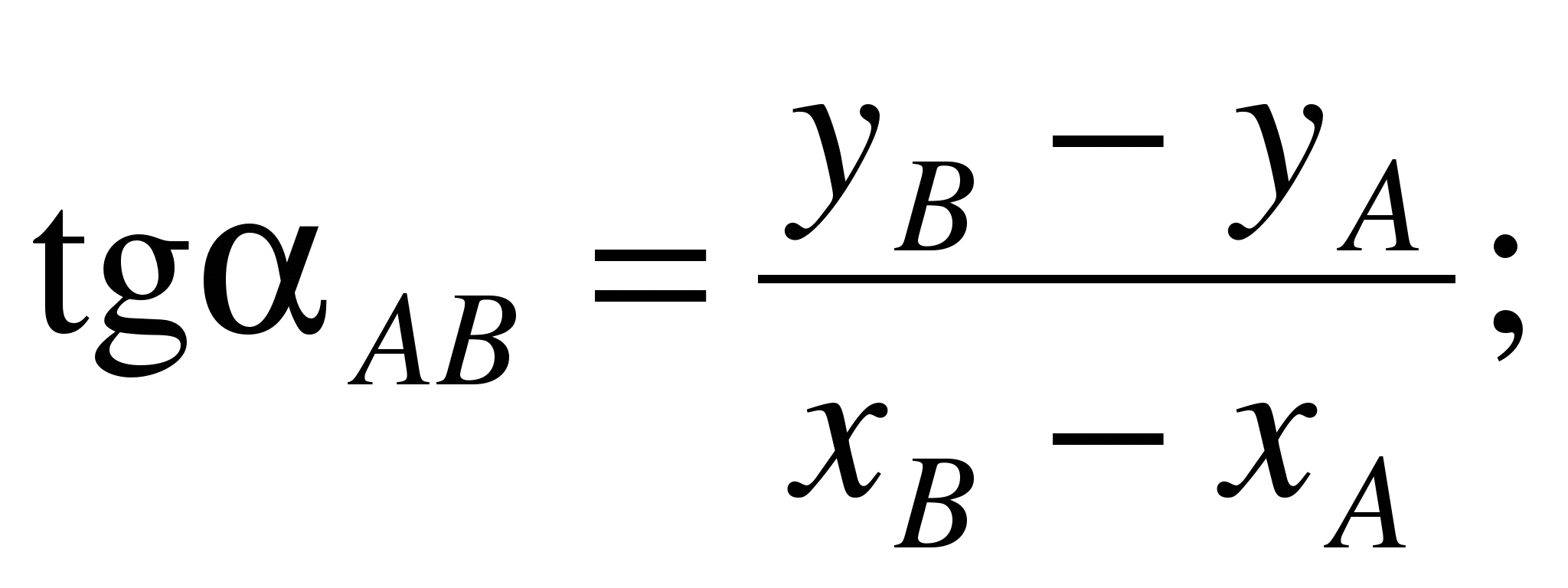
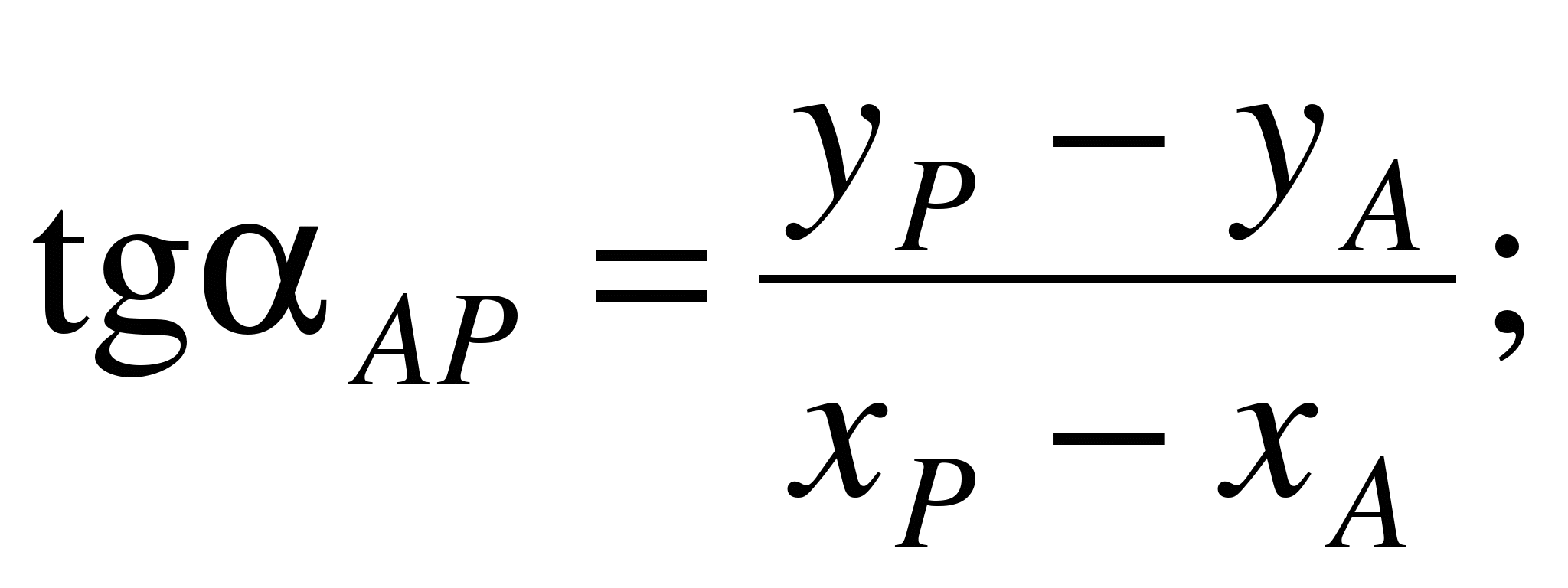
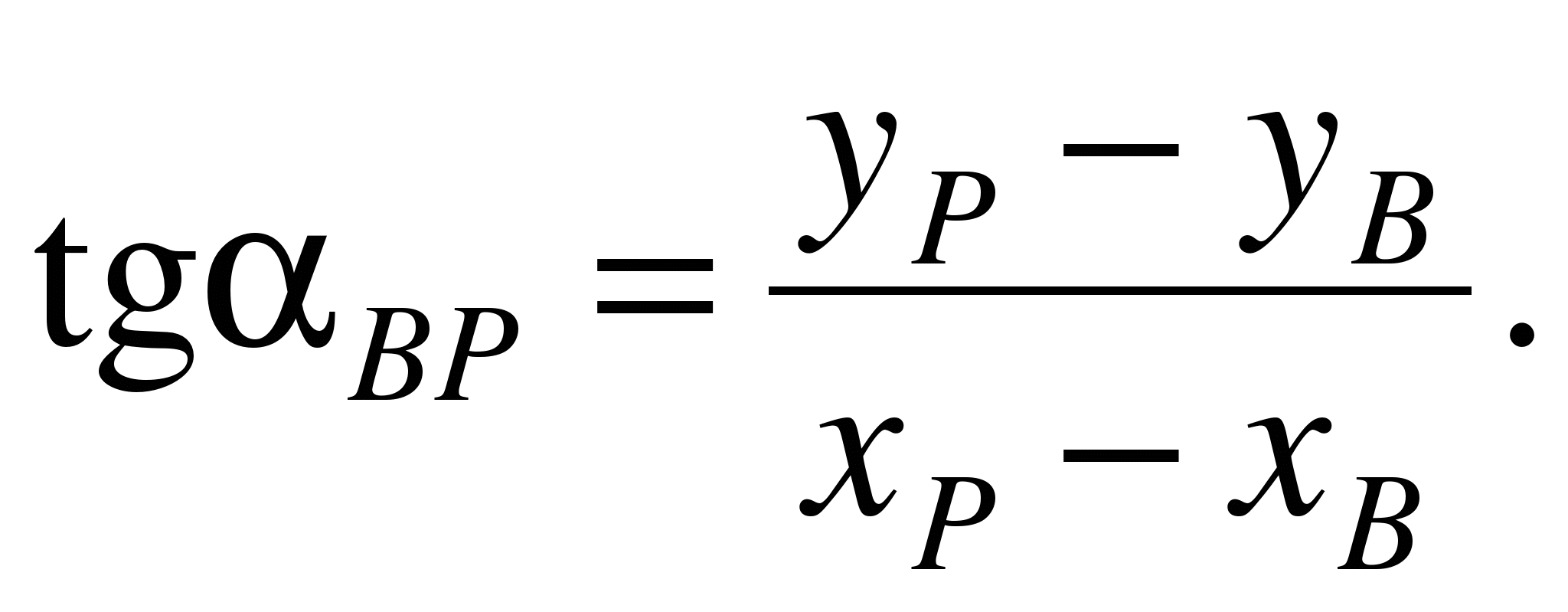 (1.27)
(1.27)
^
 2020-08-05
2020-08-05 127
127

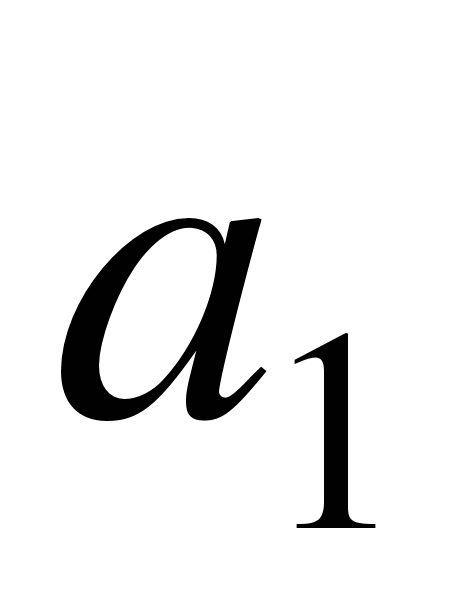 и
и 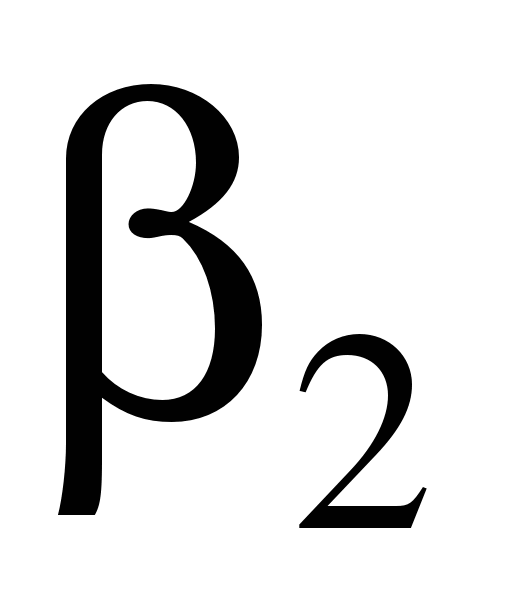 и фиксируют направление точками
и фиксируют направление точками 






