2020-08-05
165
Геометрические построения – это способ решения задач, при котором ответ получают графическим путем. К ним относятся: деление отрезка, угла, окружности на равные части, построение сопряжения, конусности и уклона.
Примеры деления окружности на равные части с помощью циркуля показаны на рис.28.
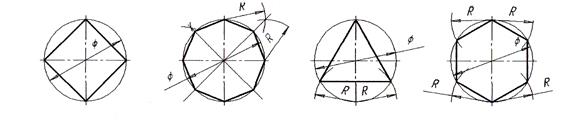
а) б) в) г)
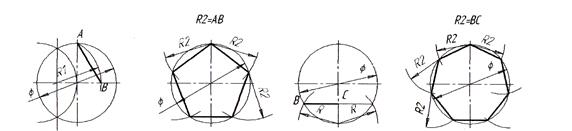
д) е) ж) з)
Рисунок 28 - Деление окружности на равные части:
а) – на 4 части; б) – на 8 частей; в) – на 3 части; г) – на 6 частей;
д), е) – на 5 частей; ж), з) – на 7 частей
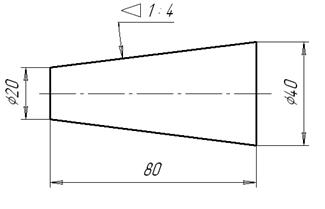Построение конусности, уклона.
|
C = (D - d) / L
Например (рис.29), если известны размеры D =40мм, d =20мм, L =80мм.
C = (40 - 20) / 80 = 1:4
На машиностроительных чертежах, как правило, известны конусность и два параметра из формулы, например диаметр d и длина L. Для того, чтобы построить заданную конусность, по формуле рассчитывают недостающий параметр – D.
D = C*L+d
| |
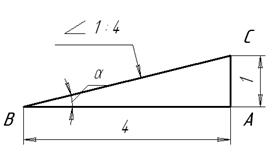Уклоном называют величину, характеризующую наклон одной прямой линии к другой прямой (выражается дробью или в процентах).
|
i = AC / AB = tga
Для построения прямой ВС (рис.30) с заданной величиной уклона к горизонтальной прямой, например 1:4 необходимо от точки А влево отложить отрезок АВ, равный четырем единицам длины, а вверх – отрезок АС, равный единице длины. Точки С и В соединяют прямой, которая дает направление искомого уклона.
|
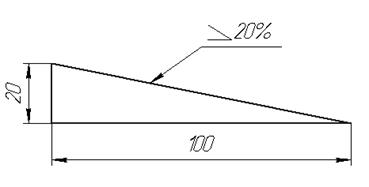Если уклон задается в процентах, например 20% (рис.31), то линия уклона строится так же, как гипотенуза прямоугольного треугольника. Длину одного из катетов принимают равной 100%, а другой – 20%, очевидно, что уклон 20% есть иначе уклон 1:5 
