Підфункції та похідні булевіх функцій, лавинний критерій SAC

ЛЕКЦІЯ 4 КРИТЕРІЇ РОЗПОВСЮДЖЕННЯ

Криптографічна практика показує, що булеві функції, що використовуються для побудови генераторів гами, крім рівноймовірності й високої нелінійності, повинні мати ряд більш тонких властивостей, які послаблюють зв’язки між виходами функцій ускладнення і послідовностями відповідних аргументів. Наявність таких властивостей у булевої функції перевіряється за допомогою, так званих, критеріїв розповсюдження та кореляційної імунності.

Розглянемо критерії розповсюдження.

Для формулювання відповідних визначень використовуються поняття підфункції булевої функції та її похідної.

Назвемо похідною булевої функції 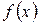 за напрямком 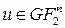, , 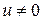функцію виду .

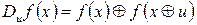Введемо також позначення , при обмеженні .

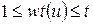Вектори 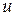, що задовільняють (у відповідному контексті) деяке обмеження будемо називати допустимими, наприклад,  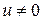для .

Підфункцією булевої функції 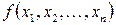, що отримана фіксацією  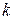змінних на місцях  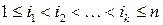за допомогою вектора 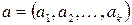, називається функція 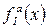, яка визначається рядками таблиці , для яких , , .

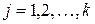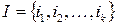Аргументами функції 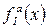 є аргументи з номерами, що не належать множині 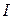, а значення  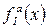дорівнює .

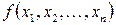Якщо функція задана аналітично, то при фіксації змінних частина змінних 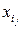 заміняється на деякі числа 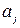, що дає нову функцію від меншої кількості змінних.

Вивчення властивостей булевих функцій з метою побудови криптосхем блокових шифрів, привело до ідеї строгого лавинного критерію (Strict Avalanche Criterion, ).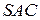

Подібні критерії відображають властивість непередбачуваності поведінки функції 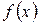 при однаковій модифікації (невідомих) аргументів.

Це означає, що при заміні (у наслідок помилки), скажимо, 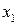 на 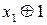, відповідні координати векторів значень функцій  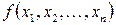і 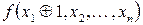 не співпадатимуть у половині випадків.

Або, наприклад, мінімальне відхилення від істинного значення аргументу 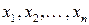 призведе до максимально швидкого, як кажуть, лавинного розповсюдження помилок у рекурентній послідовності .

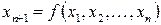Булева функція 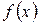 задовольняє строгому лавинному критерію 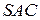, якщо  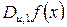- рівноймовірна функція для всіх допустимих .

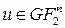Цей підхід спрямований на побудову функцій, для яких наявність значень частини аргумента не впливає на складність визначення решти змінних з тих чи інших співвідношень статистичними методами.

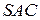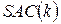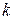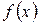Узагальненням  є  - строгий лавинний критерій порядку , . Функція  задовольняє 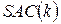, якщо  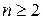і будь-яка її підфункція 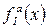, отримана фіксацією  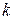змінних, задовольняє звичайному критерію .

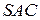Оскільки в самому 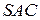 змінні не фіксуються, то для критерію  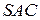часто використовується позначення .

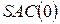Можна показати, що якщо функція задовільняє 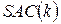, то вона задовільняє , де .