В критерії 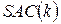 , за визначенням, у підфункцій допускається модифікація довільного, але тільки одного з аргументів.
, за визначенням, у підфункцій допускається модифікація довільного, але тільки одного з аргументів.
Модифікація декількох аргументів розглядається в так званому критерії розповсюдження 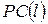 степеня
степеня 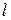 (Propagation Criterion).
(Propagation Criterion).
Булева функція 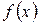 задовольняє критерій розповсюдження
задовольняє критерій розповсюдження 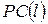 степеня
степеня 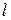 , якщо будь-яка її похідна
, якщо будь-яка її похідна 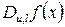 ,
, 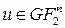 рівноймовірна.
рівноймовірна.
У випадку, коли відомо, що 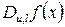 рівноймовірна для конкретного вектора
рівноймовірна для конкретного вектора 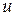 , говорять, що
, говорять, що 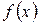 задовольняє критерій розповсюдження
задовольняє критерій розповсюдження 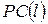 степеня
степеня 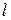 відносно вектора
відносно вектора 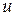 .
.
Загальний випадок відповідає формулюванню критерія розповсюдження степеня 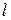 , порядку
, порядку 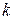 .
.
Функція 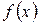 задовольняє критерій розповсюдження
задовольняє критерій розповсюдження 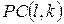 степеня
степеня 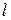 , порядку
, порядку 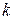 ,
, 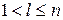 ,
, 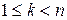 , якщо для будь-якої з підфункцій
, якщо для будь-якої з підфункцій 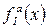 , отриманих фіксацією
, отриманих фіксацією 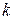 змінних, всі похідні
змінних, всі похідні 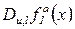 ,
, 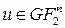 , рівноймовірні.
, рівноймовірні.
Порада. Позначення 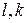 - стандартні, звикнути до них простіше, якщо співставляти їм мнемонічні назви «допустима вага» «фіксація».
- стандартні, звикнути до них простіше, якщо співставляти їм мнемонічні назви «допустима вага» «фіксація».
Приклади
Запишемо булеву функцію 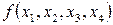
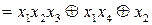 у табличному виді, та обчислимо її похідні
у табличному виді, та обчислимо її похідні 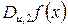 для
для 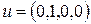 і
і 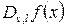 при
при 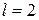 ,
, 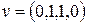 . Тобто, ми обчислимо не всі похідні другого порядку, а деякі.
. Тобто, ми обчислимо не всі похідні другого порядку, а деякі.
Таблиця 5.1 Похідні булевих функцій
| № | 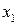
| 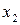
| 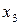
| 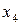
| 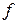
| 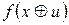
| 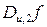
| 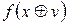
| 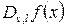
|
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 3 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 5 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 7 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| A | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| B | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| C | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| D | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| E | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| F | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
Підфункції 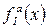 від двох змінних при
від двох змінних при 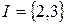 .
.
Оскількі розмірність 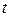 аргументу підфункцій (тобто, після фіксації) дорівнює 2, то кількість змінних, що фіксуються дорівнює
аргументу підфункцій (тобто, після фіксації) дорівнює 2, то кількість змінних, що фіксуються дорівнює 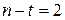 . Таким чином, умова
. Таким чином, умова 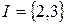 коректна. Якщо
коректна. Якщо 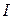 не було би задано, то слід було б вибирати чотири вектори
не було би задано, то слід було б вибирати чотири вектори 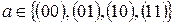 для чотирьох значень
для чотирьох значень 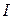 .
.
Таблиця 5.2 Підфункції, що отримані з 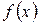 при
при 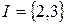
| № | 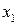
| 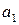
| 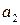
| 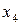
| 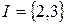 , , 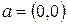 , , 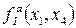
| |
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 1 | 0 | |
| 8 | 1 | 0 | 0 | 0 | 0 | |
| 9 | 1 | 0 | 0 | 1 | 1 | |
| № | 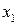
| 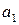
| 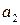
| 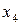
| 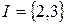 , , 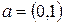 , , 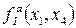
| |
| 2 | 0 | 0 | 1 | 0 | 0 | |
| 3 | 0 | 0 | 1 | 1 | 0 | |
| A | 1 | 0 | 1 | 0 | 0 | |
| B | 1 | 0 | 1 | 1 | 1 | |
| № | 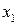
| 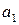
| 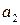
| 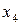
| 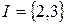 , , 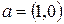 , , 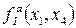
| |
| 4 | 0 | 1 | 0 | 0 | 1 | |
| 5 | 0 | 1 | 0 | 1 | 1 | |
| С | 1 | 1 | 0 | 0 | 1 | |
| В | 1 | 1 | 0 | 1 | 0 | |
| № | 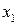
| 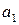
| 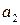
| 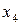
|
| |
| 6 | 0 | 1 | 1 | 0 | 1 | |
| 7 | 0 | 1 | 1 | 1 | 1 | |
| E | 1 | 1 | 1 | 0 | 0 | |
| F | 1 | 1 | 1 | 1 | 1 | |
Критерій 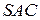 . Необхідно, щоб похідна
. Необхідно, щоб похідна 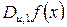 була рівноймовірною для всіх допустимих
була рівноймовірною для всіх допустимих 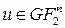 . Допустимими є чотири вектори з вагою одиниця.
. Допустимими є чотири вектори з вагою одиниця.
Один з них: 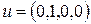 . Похідну
. Похідну 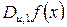 ми вже обчислили як приклад похідної
ми вже обчислили як приклад похідної 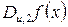 . Кількість одиниць у векторі значень функції
. Кількість одиниць у векторі значень функції 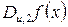 дорівнює 12, а не 8, таким чином, одна з похідних не є рівноймовірною і
дорівнює 12, а не 8, таким чином, одна з похідних не є рівноймовірною і 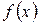 не задовілняє
не задовілняє 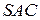 .
.
Критерій 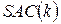 . Нехай
. Нехай 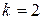 , тобто фіксуються 2 змінні.
, тобто фіксуються 2 змінні.
Розглянемо підфункцію 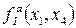 для
для 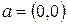 ,
, 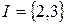 (табл. 5.2) і застосуємо до неї критерій
(табл. 5.2) і застосуємо до неї критерій 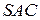 (табл. 5.3).
(табл. 5.3).
Маємо випробувати вектори з вагою одиниця. Нехай 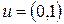 ,
, 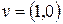 .
.
Таблиця 5.3 Критерій 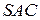 для підфункції від двох змінних
для підфункції від двох змінних
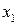
| 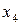
| 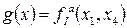
| 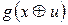 , , 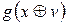
| 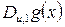 , , 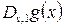
|
| 0 | 0 | 0 | 0 0 | 0 0 |
| 0 | 1 | 0 | 0 1 | 0 1 |
| 1 | 0 | 0 | 1 0 | 1 0 |
| 1 | 1 | 1 | 0 0 | 1 1 |
Похідні 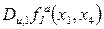 і
і 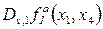 є рівноймовірними, тому треба продовжити обчислення для інших підфункцій.
є рівноймовірними, тому треба продовжити обчислення для інших підфункцій.
Оскільки при 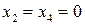 функція
функція 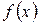
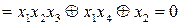 , то для
, то для 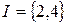 і
і 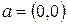
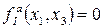 . Звідки випливає, що всі похідні цієї підфункції, зокрема,
. Звідки випливає, що всі похідні цієї підфункції, зокрема, 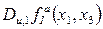 , дорівнюють нулю, тобто, не є рівноймовірними. Таким чином,
, дорівнюють нулю, тобто, не є рівноймовірними. Таким чином, 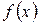 не задовільняє
не задовільняє 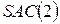 .
.
Критерій розповсюдження 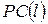 ,
, 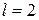 .
.
Для цього критерія довільна похідна 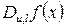 має бути рівноймовірною.
має бути рівноймовірною.
Ми обчислили 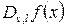 при
при 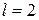 ,
, 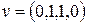 і знайшли, що вектор значень цієї функції містить 10 одиниць (табл 5.1), тобто,
і знайшли, що вектор значень цієї функції містить 10 одиниць (табл 5.1), тобто, 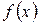 не задовільняє
не задовільняє 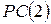 .
.
Критерій розповсюдження 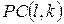 степеня
степеня 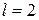 , порядку
, порядку 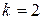 .
.
Для цього критерія всі похідні 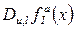 ,
, 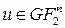 для всіх підфункції
для всіх підфункції 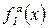 , що отримані фіксацією
, що отримані фіксацією 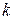 змінних, мають бути рівноймовірні.
змінних, мають бути рівноймовірні.
Ми вже знаємо, що 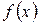 не задовільняє
не задовільняє 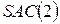 , тому існують похідні
, тому існують похідні 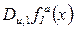 , які не є рівноймовірними, звідки випливає що серед множини похідних
, які не є рівноймовірними, звідки випливає що серед множини похідних 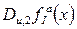 не всі рівноймовірні, тому
не всі рівноймовірні, тому 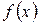 не задовільняє
не задовільняє 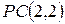 .
.
 2020-08-05
2020-08-05 102
102
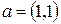 ,
, 






