Что такое поверхностное моделирование и где оно используется.
Данный метод моделирования нашел широкое применение в САПР автомобильной и авиационной промышленности, для проектирования пресс-форм и штампов, при дизайне выкройки для производства одежды и обуви, в стекольной промышленности, при проектировании пресс-форм для пластмассовых изделий. Поверхностная модель создается путем математического описания поверхностей, заключенных между ребрами детали. Эти описания помещаются в банк данных детали в качестве дополняющих геометрических элементов. Графически поверхности могут представляться сеткой или теневым рисунком. С помощью поверхностных моделей можно вычислять площади сечений, поверхностей, воспроизводить форму детали. Эти модели используют для проверки правильности геометрии сборок, при проектировании сложных ЗБ-поверхностей. Проблемой при использовании поверхностных моделей является обозначение размеров и штриховки, эти модели не содержат описания внутренней структуры объекта и не могут быть использованы в программах инженерного анализа, таких как конечно-элементный анализ распределения температур, внутренних напряжений и деформаций.
1. Современные методы проектирования поверхностей позволяют строить объекты, основываясь на минимальном количестве исходных данных:
2. а) поверхность по траектории (лофтинг (loft или lofting) - метод построения галереи (“труба”)) получается движением эскиза вдоль криволинейной образующей и произвольного числа направляющих кривых, деформирующих исходный контур;
3. б) поверхность вращения получается вращением произвольного профиля относительно оси;
4. в) поверхность вытяжки (выдавливание) получается плоскопараллельным вытягиванием замкнутого или разомкнутого эскиза в направлении, перпендикулярном плоскости эскиза, или под произвольным углом.
Векторный способ задания точки на плоскости.
 Точку на плоскости будем описывать с помощью радиус-вектора r = [x, y],компоненты которого равны её координатам.
Точку на плоскости будем описывать с помощью радиус-вектора r = [x, y],компоненты которого равны её координатам.
Как расположены векторы N и t при правой ориентации?
При правой ориентации нормали, т. е. при движении точки по линии, вектор N направлен перпендикулярно вправо от вектора т, связь векторов нормали и направления прямой будет следующей: т = [ - Ny Nx], N = [ty -tx].
Записать условие коллинеарности трех точек r1, r2, r3.
a) 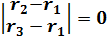 – три точки лежат на одной прямой;
– три точки лежат на одной прямой;
b) 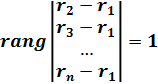 – обобщение на произвольное число точек r1 ÷ rn;
– обобщение на произвольное число точек r1 ÷ rn;
c) 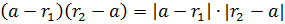 - точка a лежит на отрезке r1r2 при нулевом угле между векторами
- точка a лежит на отрезке r1r2 при нулевом угле между векторами 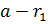 и
и 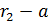 , где
, где 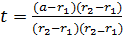 – значение параметра, соответствующее положение точки a=r1 + (r2-r1)t на прямой относительно её отрезка r1r2.
– значение параметра, соответствующее положение точки a=r1 + (r2-r1)t на прямой относительно её отрезка r1r2.
5. Какая точка называется геометрическим центром треугольника.
Геометрический центр треугольника расположен в точке пересечения его медиан и делит каждую из них в отношении 2:1 от вершины, из которой проведена медиана
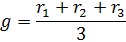
6. Записать уравнение плоскости, заданной вектором F=[A B C D].
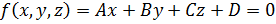
7. Перечислить возможные расположения плоскостей.
Плоскости могут быть параллельными, пересекающимися и перпендикулярными друг к другу.
8. Что называется геометрическим преобразованием?
Примеры геометрических преобразований — это повороты, отражения относительно точки, прямой, плоскости, переносы вдоль прямой или вдоль плоскости, подобие, сжатие и другие.
9. Дать определение полигона.
Полигон - многоугольник, заданный списком точек-вершин в порядке их обхода по замкнутому контуру r1→r2→…→rn→r1 или Р = {r1r2…rnr1} Треугольник - простейший полигон {r1r2r3r1}.
10. Записать каноническое уравнение двуполостного гиперболоида.
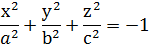
11. 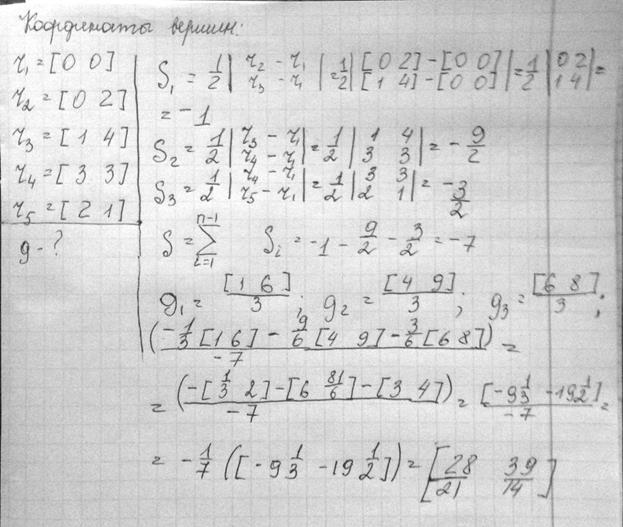 Найти геометрический центр полигона P={r1r2…r5r1}, если
Найти геометрический центр полигона P={r1r2…r5r1}, если
r1=[0 0], r2=[0 2], r3=[1 4], r4=[3 3], r5=[2 1].
 2020-08-05
2020-08-05 89
89






