Орбитальный магнитный момент. В квантовой теории магнитный момент μ и механический момент М атома следует заменить операторами 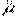 и
и 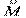 :
:
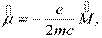 
| (13.46) |
Отсюда следует, что изучение свойств магнитного момента электрона сводится к изучению свойств операторов 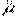 и
и 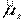 . А так как операторы
. А так как операторы 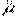 и
и 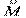 ,
,  и
и 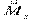 отличаются друг от друга только постоянным множителем, то их свойства совершенно аналогичны: магнитный и механический моменты квантуются по одинаковым правилам.
отличаются друг от друга только постоянным множителем, то их свойства совершенно аналогичны: магнитный и механический моменты квантуются по одинаковым правилам.
В стационарном состоянии определенные значения могут иметь только модуль магнитного момента  и одна из его проекций на произвольную ось Z. Имея в виду (13.46), а также (13.34) и (13.36), запишем собственные значения операторов
и одна из его проекций на произвольную ось Z. Имея в виду (13.46), а также (13.34) и (13.36), запишем собственные значения операторов 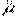 и
и 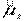 :
:
 L = 0, 1, 2,... L = 0, 1, 2,...
|
| |
|
| (13.48) | |
где μБ — магнетон Бора: μБ = eћ/2mc. Он играет роль кванта магнитного момента (точнее его проекции μz).
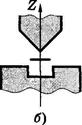
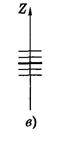
Опыты Штерна и Герлаха. Наличие у атомов магнитных моментов и их квантование было доказано экспериментально Штерном и Герлахом (1921). В их опытах пучок атомов пропускался сквозь сильно неоднородное поперечное магнитное поле (рис. 13.10, а). Необходимая степень неоднородности поля достигалась с помощью специальной формы полюсных наконечников N и S электромагнита (рис. 13.10, б). После прохождения магнитного поля пучок атомов попадал на фотопластинку Р и оставлял на ней след.
|
|
|
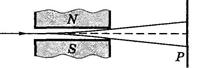
а)
Рис. 13.10.
Если атомы обладают магнитным моментом, то согласно электродинамике на них будет действовать сила, проекция которой на ось Z (см. рис. 13.10, б)

| (13.49) |
где μ z — проекция магнитного момента атома на ось Z. Из этой формулы видно, что для получения необходимого эффекта при малых значениях μ z нужно обеспечить достаточно большую неоднородность поля, т. е. ∂Bz/∂z. Это и достигалось с помощью указанной формы полюсных наконечников.
В отсутствие магнитного поля след пучка на фотопластинке ^ Р имел вид одной полоски (z = 0). При включении же магнитного поля наблюдалось расщепление пучка (рис. 13.10, в), что являлось следствием квантования проекции магнитного момента μ z в формуле (13.49): μ z может принимать только ряд дискретных значений. В опытах обнаружилось также, что для разных атомов число компонент, на которые расщеплялся пучок, было или нечетным, или четным. Анализ полученных результатов показал, что нечетное число компонент возникает у атомов, обладающих только орбитальным механическим моментом ML, тогда магнитное поле снимает вырождение по L и число компонент (значений mL) будет равно 2 L + 1, т. е. нечетным.
Если же момент атома является суммой орбитального и спинового, т. е. определяется квантовым числом ^ J, то число компонент будет равно 2 J + 1, и в зависимости от того, полуцелым или целым будет значение J, число компонент будет соответственно четным или нечетным.
|
|
|
^ Спиновый магнитный момент. Зная степень неоднородности магнитного поля, т. е. дВг/дг, Штерн и Герлах по величине расщепления пучка на фотопластинке рассчитали значение проекции спинового магнитного момента на направление магнитного поля, μB. Выяснилось, что μB равен одному магнетону Бора. Этот результат приводит к гиромагнитному отношению вдвое превышающему гиромагнитное отношене для орбитальных моментов. В связи с этим говорят, что спин обладает удвоенным магнетизмом.
Итак, спиновый магнитный момент и его проекция на произвольную ось Z определяются как
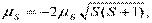
| (13.50) |
| μSz = -2 μБ ms, ms=S,S- 1, …, -S. | (13.51) |
При S = 1/2 ms = +1/2 и -1/2.
Принято говорить, что спиновый магнитный момент электрона равен одному магнетону Бора. Такая терминология обусловлена тем, что при измерении магнитного момента мы обычно измеряем его проекцию, а она как раз и равна одному μ Б. Опыты Штерна и Герлаха явились еще одним убедительным доказательством наличия у электрона спина. Помимо этих опытов следует упомянуть и о так называемых магнитомеханических явлениях — опытах Эйнштейна и де Хааса, а также опыте Барнетта. И в этих опытах было обнаружено, что гиромагнитное отношение спиновых моментов тоже вдвое больше отношения орбитальных.
^ Полный магнитный момент атома. Вследствие удвоенного магнетизма спина гиромагнитное отношение полных моментов μ/MJ оказывается значительно более сложным. Оно зависит от квантовых чисел L, S и J. Соответствующий расчет, проводимый в квантовой теории, позволил найти магнитный момент μ и его проекцию на ось Z:
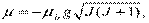
| (13.52) |
| μ z = - μ Б gmJ, mJ = J, J -1, …, - J, | (13.53) |
где g — множитель (или фактор) Ланде
В частности, в синглетных состояниях (S = 0) J = L, g = 1, и мы приходим к формулам (13.47) и (13.48). А при L = 0 (J = S, g = 2) — к формулам (13.50) и (13.51).
^ 13.9. Атом во внешнем магнитном поле. Эффект Зеемана
Расщепление в магнитном поле энергетических уравнений атомов, приводящее к расщеплению спектральных линий в спектрах, называют эффектом Зеемана. Различают эффект Зеемана: нормальный (простой), когда каждая линия расщепляется на три компонента, и аномальный (сложный), когда каждая линия расщепляется на большее, чем три, число компонентов.
Эффект Зеемана характерен для атомов парамагнетиков, так как только эти атомы обладают отличным от нуля магнитным моментом и могут взаимодействовать с внешним магнитным полем.
Атом, обладающий магнитным моментом, приобретает в магнитном поле дополнительную энергию
| ∆ E = - μ JB B, | (13.54) |
где μ JB — проекция полного магнитного момента атома на направление поля В. Имея в виду формулу (13.53), запишем выражение для энергии каждого подуровня:
| E = E 0 + ∆ E = E 0 + μ Б gBmJ, mJ = J, J -1, …, - J, | (13.55) |
где Е0 — энергия уровня в отсутствие магнитного поля.
Отсюда следует, что уровни с квантовым числом ^ J расщепляются в магнитном поле на 2J + 1 равноотстоящих друг от друга подуровней, причем величина расщепления зависит от множителя Ланде g, т. е. интервалы δЕ между соседними подуровнями пропорциональны g: δЕ ≈ g. Таким образом, магнитное поле в результате расщепления уровней снимает вырождение по mJ.
Кроме этого, необходимо учесть, что возможны только такие переходы между подуровнями, принадлежащими разным уровням, при которых выполняются следующие правила отбора для квантового числа тJ:
| ∆ mJ = 0, ±1. | (13.56) |
Если в (13.55) B = 0, то энергетический уровень определяется только первым членом, если В ≠ 0, то необходимо учитывать возможные значения mJ, а оно может принимать 2 J + 1 значений. Это означает расщепление первоначального энергетического уровня на 2 J + 1 подуровней.
|
|
|
Теперь можно понять происхождение мультиплетов Зеемана. На рис. 13.11 рассмотрены возможные переходы в атоме водорода между состояниями р (l = 1)иs(l =0) для двух случаев:
когда В = 0 (внешнее магнитное поле отсутствует);
когда В ≠ 0.
В 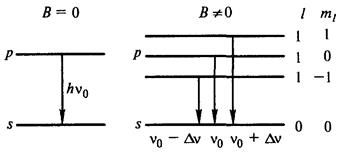 отсутствие поля наблюдается одна линия с частотой v 0. В магнитном поле p -состояние расщепляется на три подуровня (при l = 1, ml, = 0, ± 1), с каждого из которых могут происходить переходы на уровень s, и каждый переход характеризуется своей частотой: v 0 - ∆ v, v 0, v 0 + ∆v. Следовательно, в спектре появляется триплет (наблюдается нормальный эффект Зеемана).
отсутствие поля наблюдается одна линия с частотой v 0. В магнитном поле p -состояние расщепляется на три подуровня (при l = 1, ml, = 0, ± 1), с каждого из которых могут происходить переходы на уровень s, и каждый переход характеризуется своей частотой: v 0 - ∆ v, v 0, v 0 + ∆v. Следовательно, в спектре появляется триплет (наблюдается нормальный эффект Зеемана).
Рис. 13.11.
Не вдаваясь в подробности, отметим, что нормальный эффект Зеемана наблюдается в том случае, если исходные линии не обладают тонкой структурой (являются синглетами). Если исходные уровни обладают тонкой структурой, то в спектре появляется большее число компонентов и наблюдается аномальный эффект Зеемана.
СПИН
Spin
Спин (от англ. spin – вращаться) – собственный момент количества движения элементарной частицы, имеющий квантовую природу и не связанный с её перемещением в пространстве как целого. Спин отвечает неотъемлемому и неизменному внутреннему вращательному состоянию, присущему частице, хотя это вращательное состояние нельзя трактовать классически – как вращение тела вокруг собственной оси. Наряду со спином, любая частица, перемещаясь как целое в пространстве (например, по замкнутой орбите) относительно некой внешней точки (центра орбиты), имеет относительно этой точки внешний или орбитальный момент количества движения.
Спин был первоначально введен для того, чтобы объяснить экспериментально наблюдаемый факт, что многие спектральные линии в атомных спектрах состоят из двух отдельно расположенных линий. Например, первая линия серии Бальмера в атоме водорода, которая проявляется при переходах между уровнями с n = 3 и n = 2, должна наблюдаться как одиночная линия с длиной волны λ = 6563 Å, однако на самом деле наблюдались две линии с расстоянием между ними Δλ = 1.4Å. Это расщепление первоначально связывалось с еще одной дополнительной степенью свободы электрона – вращением. Предполагалось, что электрон можно рассматривать как классический вращающийся волчок, и величина спин связывалась с его характеристикой вращения. На самом деле, как выяснилось позже, спин имеет квантовую природу и не связан с какими-либо перемещениями частицы в пространстве. Величина вектора спина 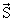 равна ћ[s(s + 1)]1/2, где ћ = h/2π (h - постоянная Планка), а s - квантовое число спина, т.е. характерное для каждой частицы полуцелое или целое положительное число (оно может быть и нулевым). Частицы с целым спином называются бозонами, с полуцелым – фермионами.
равна ћ[s(s + 1)]1/2, где ћ = h/2π (h - постоянная Планка), а s - квантовое число спина, т.е. характерное для каждой частицы полуцелое или целое положительное число (оно может быть и нулевым). Частицы с целым спином называются бозонами, с полуцелым – фермионами.
Переносчики взаимодействий γ-квант, W±-, Z-бозоны и 8 глюонов имеют спин s = 1 и являются бозонами. Лептоны e, μ, τ, νe, νμ, ντ, кварки u, d, s, c, b, t имеют спин s = 1/2 и являются фермионами.
Понятие спина применяют и к сложным, составным микрообъектам – атомам, атомным ядрам, адронам. В этом случае под спином J понимают момент количества движения микрообъекта в состоянии покоя, т.е. когда орбитальный (внешний) момент количества движения микрообъекта  = 0. Спины составных микрообъектов являются векторной суммой спиновых
= 0. Спины составных микрообъектов являются векторной суммой спиновых  и орбитальных
и орбитальных  моментов входящих в их состав частиц – ядра и электронов в случае атома, протонов и нейтронов в случае ядра, кварков и глюонов в случае протона, нейтрона и других адронов. Спин частицы однозначно связан со статистикой, которой подчиняется ансамбль частиц с данным спином. Все частицы с целым и нулевым спином подчиняются статистике Бозе-Эйнштейна. Частицы полуцелым спином подчиняются статистике Ферми-Дирака.
моментов входящих в их состав частиц – ядра и электронов в случае атома, протонов и нейтронов в случае ядра, кварков и глюонов в случае протона, нейтрона и других адронов. Спин частицы однозначно связан со статистикой, которой подчиняется ансамбль частиц с данным спином. Все частицы с целым и нулевым спином подчиняются статистике Бозе-Эйнштейна. Частицы полуцелым спином подчиняются статистике Ферми-Дирака.
|
|
|
СПИНОВОЕ КВАНТОВОЕ ЧИСЛО - квантовое число, определяющее величину спина квантовой системы (атома, иона, атомного ядра, молекулы), т. е. её собств. (внутр.) момента кол-ва движения (момента импульса). Спиновый момент импульса s квантуется: его квадрат определяется выражением 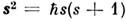 , где s - С. к. ч. (называемое часто просто спином). Проекция вектора s на произвольное направление z также квантуется: для частиц с ненулевой массой
, где s - С. к. ч. (называемое часто просто спином). Проекция вектора s на произвольное направление z также квантуется: для частиц с ненулевой массой 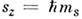 (где ms - магнитное спиновое число), т. е. принимает 2s + 1 значений. Число s может принимать целые, нулевые или полуцелые значения.
(где ms - магнитное спиновое число), т. е. принимает 2s + 1 значений. Число s может принимать целые, нулевые или полуцелые значения.
 2020-08-05
2020-08-05 261
261








