Скалярный квадрат вектора.Свойства скалярного произведения

Два вектора сонаправлены.

 В этом случае угол между ними равен нулю, , и формула скалярного произведения принимает вид: .

А что будет, если вектор умножить на самого себя? Понятно, что вектор сонаправлен сам с собой, поэтому пользуемся вышеуказанной упрощенной формулой:

Или:

Число называется скалярным квадратом вектора , и обозначатся как .

Таким образом, скалярный квадрат вектора равен квадрату длины данного вектора:

Из данного равенства можно получить формул у для вычисления длины вектора:

Свойства скалярного произведения.

Для произвольных векторов и любого числа справедливы следующие свойства:

1) – переместительный или коммутативный закон скалярного произведения.

2) – распределительный или дистрибутивный закон скалярного произведения. Попросту, можно раскрывать скобки.

3) – сочетательный или ассоциативный закон скалярного произведения. Константу можно вынести из скалярного произведения.

, что можно делать, а чего нельзя.

Пример 3

Найти скалярное произведение векторов и , если известно, что .

Решение:

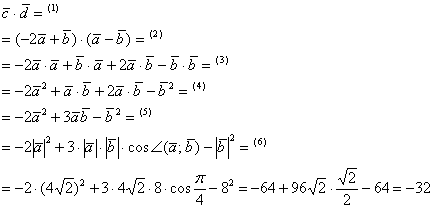
  Ответ:

Пример 4

Найти скалярное произведение векторов и , если известно, что .

Решение:

Ответ:

Пример 5

Найти длину вектора , если .

Решение будет следующим:

(1) Поставляем выражение вектора .

(2) Используем формулу длины: , при этом в качестве вектора «вэ» у нас выступает целое выражение .

(3) Используем школьную формулу квадрата суммы Или – получилось то же самое с точностью до перестановки слагаемых.

Ответ:

Угол между векторами

Скалярное произведение векторов равно .,т.е.

А части поменяем местами:

Если известен косинус угла: , то с помощью обратной функции легко найти и сам угол: .

Пример 5

Найти угол между векторами и , если известно, что .

Решение: Используем формулу:

Итак, если , то :

 

Ответ: