Показатели точности математического моделирования движения КА вокруг центра масс

Формирование высокоточной математической модели движения КА вокруг центра масс заданной точности

Как отмечалось в предыдущей работе [1], облик математической модели функционирования систем КА, в частности модели движения КА определяется:

· целью управляемого движения,

· требованиями точности реализации целей движения.

Первый фактор по существу формирует цель и задачи моделирования, а второй – определяет уровень требований к модели. При этом связь между задачей управляемого движения и задачей моделирования этого процесса очевидна, поскольку использование математической модели как инструмента целенаправленного исследования должно быть переподчинено этой же цели.

Очевидно также, что математических моделей, удовлетворяющих заданному конкретному уровню требований точности (типа неравенства), – бесконечное множество, поскольку чем полнее модель отражает существующую реальность, тем она с большим запасом удовлетворяет этим требованиям. Однако процесс уточнения модели бесконечен (в силу бесконечной сложности любого физического процесса) и поэтому должны быть установлены разумные границы наращивания модели, позволяющие:

· с одно стороны, обеспечивать требуемую точность моделирования;

· а с другой стороны, не перегружать понапрасну вычислительный процесс несущественными составляющими модели, которые могут оказаться весьма сложными с математической точки зрения.

Таким образом, при формировании математической модели движения КА вокруг центра масс необходимо стремится к рациональной математической модели, которая при максимальной простоте (как по форме, так и по содержанию) обеспечивает заданные требования точности моделирования [1].

Показатели точности математического моделирования движения КА вокруг центра масс

Характерными показателями точности движения КА вокруг центра масс являются: отклонения от реальных углов и угловых скоростей связанной с КА системы координат относительно какой-либо системы отсчета (условно инерциальной или неинерциальной).

При этом необходимо различать текущие (фазовые) показатели точности и функциональные показатели точности, последние из которых фиксируются либо в некоторые заданные моменты времени (например, в конечный момент времени), либо при достижении некоторого заданного множества состояний системы (например, целевого множесства).

Известным антиподом понятия точность моделирования – степень близости результата моделирования некоторого показателя к реальному его значению (например, углового положения КА) – является погрешность моделирования [1].

Математически функциональную погрешность моделирования можно определить, например, следующим образом.

Dj(t) = | j(R)(t) - j (M)(t) |m

(1.1)

Где m - целая степень нормы; t - может быть любым моментом времени из интервала моделирования [t₀, t_k], в том числе конечный момент времени - t_k, т.е.

Dj (k) = | j (R)(tk) - j (M)(tk) |m

(1.2)

Этот пример оценки погрешности модели может быть применен только для детерминированных динамических систем, т.е., если фазовые состояния системы и соответствующие состояния реального процесса являются детерминированными функциями времени.

В общем случае, в силу случайной природы или бесконечной сложности реальных физических процессов функционалы (1.1) и (1.2) являются случайными величинами и поэтому не могут служить в качестве показателей погрешности математических моделей в представленном виде. Кроме того, сама формируемая динамическая система может включать стохастические уравнения и тогда обе сравниваемые функции j^(R)(t) и j^(M)(t) будут случайными. В такой, более сложной ситуации точность погрешности математического моделирования характеризуется функцией распределения вероятностей одного из перечисленных функционалов. Если функция реального распределения вероятности функционалов (1.1) - (1.2) близка к нормальному (гауссовому) закону, то в качестве оценок точности моделирования могут быть использованы моментные характеристики распределения: математическое ожидание и дисперсия или среднеквадратическое отклонение (СКО), например для функционала (1.2) будем иметь:

MDj (k) = M [ j (k) ]; DDj (k) = M [(j (k) - MDj (k))2 ], sDj (k) =

(1.3)

Где M_Dj^(k), D_Dj^(k) и s_Dj^(k) – соответственно, математическое ожидание, дисперсия и СКО разбросов отклонений модельных конечных угловых положений системы от реальных.

В общем случае требования к точности математической модели можно представить в виде

Dj   ≤ eDj

(1.4)

где Dj - является показателем погрешности моделирования, а e_Dj - предельно допустимая величина этого показателя, характеризующая точность формируемой математической модели.

Анализ точности динамических систем, основанный на сравнении с результатами экспериментального полета КА, пока весьма проблематичен. Это связано с тем, что проведение летных экспериментов в космосе и атмосферах планет с целью сравнения результатов моделирования с реальным полетом КА очень дорогостоящее и технически сложно осуществимое мероприятие. Единственный путь, который доступен на современном уровне исследований космического пространства - это сравнительный анализ различных математических моделей движения КА и оценка их относительной погрешности.

Формально относительные показатели погрешности будут иметь вид, аналогичный выражениям (1.2) - (1.3), только вместо фазовых координат реального процесса, помеченных индексом "R", необходимо использовать фазовые координаты так называемых эталонных математических моделей, которые помечаются индексом "Э" и служат для получения сравнительной оценки погрешности формируемой модели. При этом необходимо иметь в виду, что эталонные модели для оценки различных факторов влияния анализируемой модели могут быть различными при одних и тех же требованиях к точности.

 

 

Например: спуск (снижение) КА в плотных слоях атмосферы планеты подвержен целому ряду возмущающих воздействий. Наиболее ощутимые из них связаны с аэродинамическими силами и моментами.

Из-за недостаточной статистической информации о плотности атмосфер планет (кроме Земли) математические модели их вариаций могут быть представлены как ограниченно-неопределенные функции. При этом разбросы вариаций плотности атмосферы, влияющие на аэродинамические силы, настолько велики, что приводят к значительным изменениям траектории спуска КА в атмосфере планет [5, 6].

В связи с этим функция вариаций плотности атмосферы планеты моделируется как одна из составляющих вектора возмущающих воздействий v_j и ограничивается рамками области неопределенности:

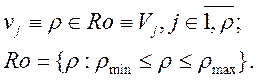
где j — номер индекса ограниченно-неопределенной вариации плотности атмосферы, которые она имеет среди других возмущений, атмосферы планеты (например: ветер, температура давление и т.д.); Р — множество возможных реализаций плотности; ρ_min, ρ_max — соответственно минимальная (разреженная) и максимальная (плотная) реализации плотности атмосферы (см. рис.1.1).

 

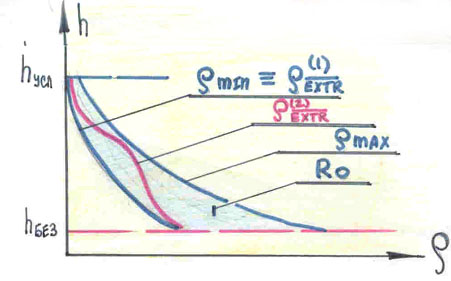
Рис.1.1

 

Аналогичным образом могут быть заданы другие ограниченно-неопределенные возмущающие воздействия, например, ветровые воздействия и проектно-баллистические характеристики КА, которые, чаще всего, с точки зрения требований к точности моделирования не могут быть представлены как детерминированные величины.

1.2. Управляющие воздействия

Продолжая пример движения КА в атмосфере планеты, управление спуском КА в плотных слоях атмосферы, как правило, осуществляется путем изменения аэродинамических сил либо по величине, либо по направлению, а иногда — того и другого одновременно.

При наличии на борту КА реактивной двигательной установки (ДУ) управление его спуском может осуществляться путем включения и выключения ДУ, изменения величины и направления вектора суммарной силы тяги ДУ.

Во всех этих вариантах управления спуском КА в атмосфере планеты на абсолютные величины составляющих вектора управления накладываются ограничения, которые по существу формируют границы множества допустимых управлений U.

Поскольку основной независимой переменной, определяющей процесс спуска КА, является время t, то какой бы сложной не оказалась, вектор-функция управления спуском она, в конечном итоге, является функцией времени. Если, например, в качестве управления выступает переменная u, тогда кусочно-непрерывные управляющие функции могут иметь виды, представленные на рис. 1.2.

Рис. 1.2

Другими словами, множество допустимых управлений U должно быть включено в класс кусочно-непрерывных функций времени (функций интегрируемых по Римону функций). В рамках этого класса функций должен вестись поиск оптимальных управлений, удовлетворяющих поставленной задаче. Формально математически это можно записать следующим образом

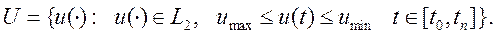
где и(·) — реализация вектор-функция управления; L₂ — класс интегрируемых по Риману функций; и _mахи u _min — максимальные и минимальные значения составляющих вектор -функции управления, соответственно.

1.3. Стратегии управления

Термин стратегия в приложении к управлению динамическими системами и, в частности, к управлению движением КА появился не случайно. Если проследить первоисточник этого термина, то им является теория военного искусства, в которой стратегия возникла как один из иерархических уровней плана ведения военных действий (доктрина, стратегия, тактика).

Согласно определению термина стратегии, который дается в энциклопедическом словаре, стратегия — это наука (искусство, способ) ведения военных действий. Другими словами, более близкими к рассматриваемой тематике, стратегия — это модель (словесная, графическая, алгоритмическая, математическая) ведения военных действий, имеющая определенный уровень детализации.

Учитывая, что стратегия как модель по уровню детализации занимает промежуточное положение между доктриной и тактикой, стратегию можно охарактеризовать как укрупнено-основополагающую модель. То есть, формирование стратегии управления динамической системой не обязательно означает определение конкретного вида функции управления с фиксированным набором параметров. В то же время, после того как стратегия управления системой задана, выбор функции управления ограничивается, иногда вплоть до выбора только параметров функции.

В самом общем случае стратегия управления может строиться в зависимости от всех факторов моделируемого движения, влияющих на достижение цели управления и на величину критерия качества управления. Точнее сказать, в зависимости от имеющейся информации об этих факторах. Однако во многих частных случаях управляемого движения динамической системы, не возникает необходимости использовать для управления системой информацию сразу обо всех значимых факторах, даже если она имеется.

Таким образом, учитывая указанные представления о понятии стратегия, можно дать следующее ее определение в контексте моделирования управляемого движения.

Стратегия управления динамической системой — это способ формирования управления системой в зависимости от реальной информации о движении системы и о внешних воздействиях на нее в реальном времени. Способ формирования может быть выражен: обычным языком, графическими средствами, математически, с помощью алгоритмических языков и др.

Исходя из данного определения, нетрудно показать, что даже в рамках допустимых управлений U можно сформировать бесконечное множество стратегий управления динамической системой.

Хотя понятие стратегии управления сравнительно недавно стало конструктивно использоваться в теории управления [16], уже давно известны и широко применяются стратегии управления, которые первоначально были применены при решении частных задач, напрямую не связанных с задачами управляемости и оптимального управления.

К таким стратегиям, прежде всего, относятся: программная стратегия управления или просто программа управления, позиционная стратегия управления или закон управления, контрстратегия управления и различные комбинированные стратегии [12, 13, 19, 23].

Программная стратегия управления отличается от всех существующих и еще не исследованных стратегий управления максимальной простотой математического описания и реализации алгоритмов управления, разработанных на ее основе. Суть программного управления заключается в том, что для определения управляющего воздействия на систему необходима реальная информация только о времени движения системы.

Программная стратегия управления может быть представлена как множество допустимых функций времени:

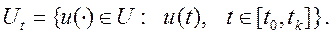
Из этого выражения видно, что функции программной стратегии управления ограничиваются только множеством допустимых управлений U, которое, как отмечалось ранее, состоит из интегрируемых (в частном случае, кусочно-непрерывных) ограниченных функцией. Единственным аргументом функций программного управления является время, получить информацию о котором не составляет труда при наличии достаточно точных часов. Если на борту КА имеется точный хронометр, то реализация программной стратегии управления полетом КА не вызывает затруднений.

Примеры программной стратегии:

Бытовые: автоматическая стиральная машина, микроволновая печь, программируемый телевизор и т.д.;

Социальные: плановое ведение хозяйства (пятилетки, семилетки и др.);

Космические: программное (по времени) включение различных систем торможения КА при спуске в атмосфере планеты.

 

Однако информации о точном времени на борту КА часто бывает недостаточно, особенно это проявляется при полетах в дальний космос, например, с целью исследования планет Солнечной системы. Дело в том, что весьма приблизительное знание условий полета не позволяет с требуемой точностью, а, следовательно, и надежностью выполнить полетное задание, т.е. решить задачу управления одним из основных условий которой является достижение целевого множества Х_с. Например, осуществить посадку КА в заданной точке поверхности планеты, используя программные стратегии управления спуском КА, удается только при очень больших размерах целевой области Х_с.

Одним из наиболее распространенных способов учета реальных условий движения системы для управления ею является использование информации о векторе фазового состояния системы - х. Известно, что динамика изменений х в полете несет в себе информацию о сложившихся в данное время реальных условиях движения [10, 11].

Позиционная стратегия управления включает в число аргументов управления не только текущее время t, но и составляющие вектора фазового состояния х:

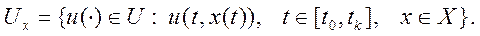
Использование позиционной стратегией управления дополнительной информации о текущем реальном состоянии системы позволяет точнее решить задачу управления движением системы. Однако прежде чем отдать предпочтение этой стратегии необходимо иметь в виду следующее:

· во-первых, если моделируемый физический процесс хорошо изучен и вследствие этого с достаточной точностью описывается детерминированной системой, то необходимость в использовании позиционной стратегии отпадает;

· во-вторых, синтез конкретных законов или алгоритмов управления в рамках позиционной стратегии представляет собой весьма сложную проблему;

· в-третьих, реализация уже синтезированных позиционных алгоритмов управления также является сложной проблемой, поскольку требует решения задачи оптимальной обработки измерений выходных функций системы с целью получения оценки текущих значений вектора ее фазового состояния.

 

Примеры позиционной стратегии:

Бытовые: холодильник, электроутюг с регулятором, сантехнический бочок и т.д.;

Социальные: рыночное ведение хозяйства (спрос ® предложение, «через» рынок);

Космические: закон управления ориентацией КА (по фактическому угловому положению КА) при наведении его на Землю, на Солнце, на звезды и др.

Обобщенная схема реализации позиционной стратегией управления - система автоматического управления КА (см. рис. 1.3)

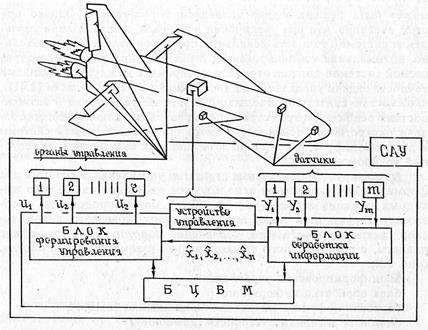
Рис. 1.3

На рисунке введены следующие обозначения:

САУ – система автоматического управления; «органы управления» - например, для воздушно-космического космического самолета (Space Shuttle): аэродинамические рули (элероны, рули высоты, рули направления), газо-реактивная система рулей; «датчики» - измерители ускорений (акселерометры), измерители угловой скорости, измерители высоты и др.; БЦВМ – бортовая цифровая вычислительная машина; u = (u₁, u₂, u₃,…, u_r) (вектор управления) - сигналы  управляющих воздействий, подающиеся на органы управления; y = (y₁, y₂, y₃,…, y_p) (вектор измерений) -  результаты измерений, получаемых с датчиков; 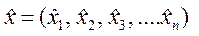 оценка вектора текущего состояния КА.

1.1.4 Общие рекомендации по практическому применению различных стратегий управления

Рекомендации по практическому применению стратегий управления представлены на рис. 1.4.

                  -- рекомендуется для регулярного применения

                   - рекомендуется для применения в частных случаях (обоснованно)

                  – используется в учебных целях.

 

 

Рис. 1.4

Применение в учебных целях необходимо для раскрытия сути методологии формирования позиционной стратегии оптимального управления.

 

Библиографический список

1) Усачов В.Е. Синтез оптимального автоматического управления организационно-техническими системам (курс лекций). М.: МАИ, 2011.

2) Усачов В.Е. Методические указания для курсовой работы по дисциплине «Синтез оптимального автоматического управления организационно-техническими системам». М.: МАИ, 2011.

3) Аоки М. Введение в методы оптимизации. М.: Наука, 1977. 344 с.

4) Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Наука, 1987.

5) Иванов Н.М., Мартынов А.И. Управление движением космических аппаратов в атмосфере Марса. – М.: Наука, 1977.

6) Иванов Н.М., Лысенко Л.Н., Мартынов А.И. Методы теории систем в задачах управления космическими аппаратами. – М.: Машиностроение, 1981.

7) Корн Г., Корн Т. Справочник по математике. - 4-е изд. - М.: Наука, 1978.

8) Красовский А.А. Справочник по теории управления. - М.: Наука, 1987.

9) Красовский Н.Н. Управление динамической системой. - М.: Наука, 1985.

10) Лебедев А.А., Красильщиков М.Н., Малышев В.В. Оптимальное управление движением космических летательных аппаратов. – М.: Машиностроение, 1974.

11) Лебедев А.А., Бобронников В.Т., Красильщиков М.Н., Малышев В.В. Статистическая динамика и оптимизация управления летательных аппаратов. – М.: Машиностроение, 1985.

12) Малышев В.В., Усачов В.Е. Математическое моделирование управляемого движения космических аппаратов. М.: Изд-во, МАИ, 1994. 84с.

13) Малышев В.В., Усачов В.Е., Тычинский Ю.Д. Математическое моделирование управляемого движения космических аппаратов (Уч. пособие для курсовой работы). М.: Изд-во, МАИ, 2001. 58с.

14) Малышев В.В. Синтез оптимального управления ЛА. М.: Изд-во МАИ, 1983. 57 с.

15) Малышев В.В., Кибзун А.И. Анализ и синтез высокоточного управления ЛА. – М.: Машиностроение, 1987.

16) Моисеев Н.Н. Элементы теории оптимальных систем. М.: Наука, 1975.

17) Усачов В.Е. Методы оптимизации организационно-технических систем (Уч. пособие). М.: Изд-во, МАИ, 2009.

18) Усачов В.Е. Методические указания для курсовой работы по дисциплине «Методы оптимизации организационно-технических систем». М.: Изд-во, МАИ, 2006.

19) Усачов В.Е. Стратегия управления динамической системой, линейной по входным воздействиям. - Рук. деп. в ВИНИТИ  21.06.90, N 3565-В90.

20) Усачов В.Е. Оптимальное управление организационно-техническими системам (курс лекций). М.: МАИ, 2007.

21) Усачов В.Е. Методические указания для курсовой работы по дисциплине «Оптимальное управление организационно-техническими системам». М.: МАИ, 2007.

22) Химмельблау Д. Прикладное нелинейное программирование. М.: Мир, 1975.

23) Субботин А.И., Ченцов А.Г. Оптимизация гарантии в задачах управления. М.: Наука, 1981.

24) Федоренко Р.П. Приближенное решение задач оптимального управления. –М.: Наука, 1978.