Гироскопическая система

Рассмотрим теперь случай, когда диссипативные (скоростные) и неконсервативные (позиционные) силы отсутствуют и будем считать, что . Тогда уравнение динамики линейной механической системы с двумя степенями свободы представляется в виде

Такие системы называют гироскопическими. Соответствующее характеристическое уравнение может быть представлено в виде:

где , параметр - квадрат элемента матрицы гироскопических сил, .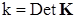

Сначала будем рассматривать случай , , 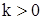и заставим параметр 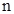изменяться от 0 до 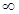. Для квадратов корней характеристического уравнения имеем

Заметим, что

Обозначим

тогда

При

Имеем четыре действительных корня, расположенных на плоскости корней симметрично по разные стороны мнимой оси (дивергенция). Такая картина имеет место при увеличении параметра до тех пор, пока .

Если

имеем две пары кратных действительных корней, расположенных симметрично относительно мнимой оси (дивергенция).

При

получаем две пары кратных чисто мнимых корней.

При возрастании параметра в пределах корни двигаются по окружности радиуса от действительной к мнимой оси, сохраняя симметрию картины относительно действительной и мнимой оси. При этом имеет место ситуация флаттера.

При , а, следовательно, и

возникают две пары сопряженных чисто мнимых корней

Состояние флаттера – раскачки при возрастании параметра перешло в состояние вибраций – колебаний конечной амплитуды. Этот эффект называют явлением гироскопической стабилизации.

Напомним, что в рассматриваемом случае , то есть