Система с позиционными силами

Лекция 1. О влиянии структуры действующих сил на устойчивость движения линейной механической системы с двумя степенями свободы

Структура сил в линейной механической системе с двумя степенями свободы

Уравнение динамики линейной механической системы с двумя степенями свободы представим в виде

                                                                  

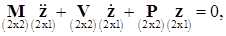
где 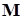 (mass) ‑ матрица инерционных коэффициентов,  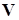(velocity) ‑ матрица скоростных сил,  (position)­ матрица позиционных сил, 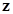 ‑ вектор обобщённых координат.

Матрица 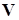 представима в виде суммы симметрической матрицы 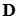, отвечающей диссипативной (скоростной) силе и кососимметрической матрицы 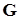, относящейся к гироскопической (скоростной) силе.

Матрица  представима в виде суммы симметрической матрицы 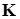, отвечающей потенциальной (позиционной) силе и кососимметрической матрицы 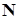, относящейся к неконсервативной (позиционной) силе.

Система с позиционными силами

Рассмотрим тот случай, когда скоростные силы отсутствуют (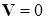) и будем считать, что 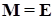. При этом уравнение динамики линейной механической системы с двумя степенями свободы будет

                                                                                

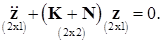
Соответствующее характеристическое уравнение может быть представлено в виде:

                                                                                      

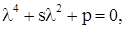
где

                                                                                

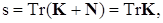
параметр 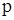 равен

                                                  

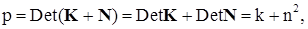
параметр 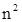 - квадрат элемента матрицы  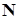неконсервативной позиционной силы, 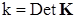. Таким образом,

                                                                                

Сначала будем рассматривать случай 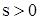, , 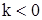и заставим параметр  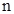изменяться от 0 до 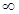. Тогда

                

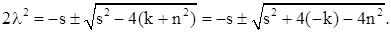
Обозначим

                                                                      

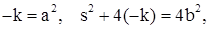
тогда

                                                                        

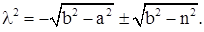
При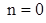

                                      

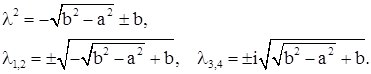
Характеристическое уравнение имеет два действительных корня, расположенных на плоскости корней симметрично по разные стороны мнимой оси, и два сопряженных чисто мнимых корня. Такая картина имеет место при увеличении параметра 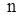 до тех пор, пока .

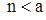Если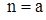

                                                              

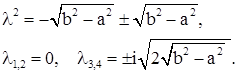
Корни оказываются на мнимой оси, и будут оставаться на ней, пока .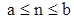

В случае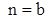

                                                      

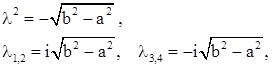
возникают две пары совпадающих чисто мнимых корней.

При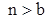

        

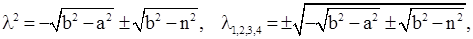
получаем две пары сопряженных комплексных корней, симметричные относительно мнимой оси.

Наличие положительных действительных корней характеризует ситуацию, которую называют дивергенция (divergence) – расхождение.

Наличие чисто мнимых (не равных нулю и не кратных) корней характеризует ситуацию, которую называют вибрации (vibration) – колебания.

Наличие комплексных корней с положительной действительной частью характеризует ситуацию, которую называют флаттер (flutter) — раскачка.

Теперь рассмотрим случай , .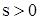

                                   

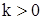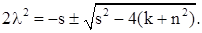
Обозначим

                                                                                   

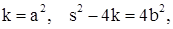
тогда

                                                                            

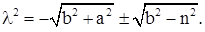
При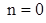

                                    

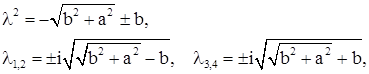
получаем две пары сопряженных чисто мнимых корней – вибрация (колебания). Такая картина имеет место при увеличении параметра 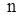 до тех пор, пока .

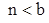Если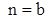

                                                      

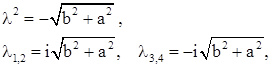
имеем две совпадающие пары сопряженных чисто мнимых корней.

При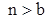

                

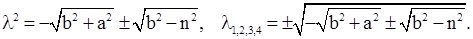
Возникают две пары сопряженных комплексных корней, симметричные относительно мнимой оси – флаттер.