2020-09-24
132
Сигналы можно сравнивать между собой, исходя из разных критериев. При передаче дискретных сообщений используется важная характеристика системы сигналов - множество расстояний между ЕЭС.
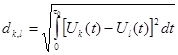
Такое определение расстояний требует, чтобы каждый сигнал 
, был финитной функцией конечной энергии на интервале от 0 до 
, вне интервала тождественно = 0.
Эти условия означают, что функция: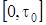 
) 
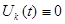при t<0
t>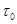 
) у этой функции конечная энергия
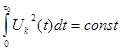
Величина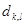 
- однозначно определяет вероятность ошибочного приёма символа, соответствующего l-го при передаче k-го. 
.
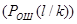Для равновероятных сигналов с модуляцией по амплитуде и фазе эта задача сводится к расположению сигнальных точек на плоскости таким образом, чтобы достигался max d при ограничении на среднюю и максимальную мощность системы сигналов.
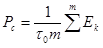
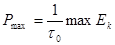
E - энергия сигнала.
Такое расположение сигнальных точек обеспечивает минимальную среднюю вероятность ошибки в каналах с гауссовской помехой и при оптимальном приеме сигналов.
Для сигналов с АМ и ФМ, когда сигнальные точки лежат на одной прямой или окружности, задача сводится к размещению всех точек симметрично. Для синусоидальных ЕЭС прямоугольной формы:
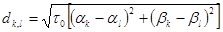
На величину d влияют ограничения расположения сигнальных точек. Например, если m=8,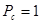 
и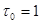 
, тогда для АМ d=0.48, при ФМ для этого же случая d=0.77 и при АФМ d=0.85. Чем больше d, тем меньше 
.
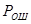При тех же условиях можно построить сетку сигналов, у которых d=0.942, не меняя свойств сигналов. Еще лучшие результаты можно получить для сигналов, которые отображаются векторами с.
Для чисто сигналов с ЧМ сигнальное расстояние зависит от количества сигналов:
При сравнении различных систем сигналов используют и другой показатель - зависимость удельной скорости передачи.
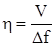, достигаемой при оптимальном приёме в канале с белым гауссовским шумом от отношения мощности сигнала и помехи 
. 
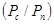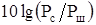
Вид таких графиков сильно зависит от вероятности ошибки.
Следовательно, лучшие результаты у КАМ и АМ ОБП, худшие при ЧМ.
