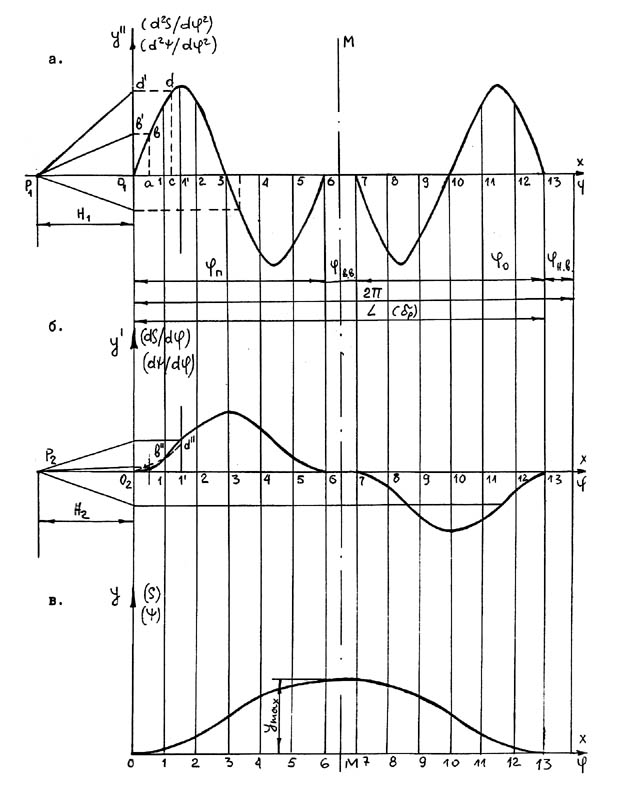
Мал. 4.3
а – первісна функція; б і в – послідовно інтегруємі функції.
Вибір масштабних коефіцієнтів при графічному інтегруванні роблять такою уявою. З огляду на, що при синтезі кулачкового механізму, вісь абсцис Х відповідає рогові повороту кулачка j, а вісь ординат - первісної (мал.4.3 а) - прискоренню вихідного елемента (d2S/dj2) або (dj2) (без указівки масштабів, у яких побудована задана крива), необхідно визначитися з масштабними коефіцієнтами функції й аргументу на графіках (мал.4.3). По осі абсцис X, як правило, відкладають відрізок довжиною L, мм, що відповідає рогові робочого профілю dp на кулачку. У цьому випадку масштабний коефіцієнт (mj(mC)) рогів повороту визначиться залежністю
mx=mj= 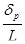 ,
,  (4.2)
(4.2)
де довжину відрізка L вибирають, як правило, пропорційної кроку розбивки DX осі абсцис.
Відомо [ 2 ], що між масштабними коефіцієнтами діаграм при графічному інтегруванні існують такі залежності (мал. 4.3)
mу=Н2×mх×m 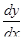
(4.3)
m 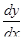 =Н1×mх×m
=Н1×mх×m 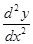
де -mу=ms; m 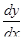 =m
=m 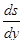 ; m
; m 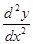 =m
=m 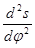
 - масштабні коефіцієнти переміщення, аналогів швидкості і прискорення штовхача для кулачкового механізму зі штовхачем, що зворотно-поступально рухаються; - масштабні коефіцієнти рогу повороту, аналогів швидкості і прискорення коромисла для кулачкового механізму з хитним коромислом.
- масштабні коефіцієнти переміщення, аналогів швидкості і прискорення штовхача для кулачкового механізму зі штовхачем, що зворотно-поступально рухаються; - масштабні коефіцієнти рогу повороту, аналогів швидкості і прискорення коромисла для кулачкового механізму з хитним коромислом.
При побудові вихідної функції 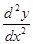 (х) і графічного інтегрування рекомендується приймати такі значення розмірів:
(х) і графічного інтегрування рекомендується приймати такі значення розмірів:
- відрізок L - від 240 мм до 360 мм;
- відрізок, що відповідає максимальному значенню 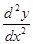 , у межах 60-100 мм;
, у межах 60-100 мм;
- відрізки Н1 і Н2, що визначають положення полюсів Р1 і Р2 у межах 40-60 мм.
- Таким чином, задавшись розмірами відрізків L, (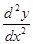 )max, Н1 і Н2 і двічі про інтегрував вихідну функцію (мал. 4.3), обчисляють один по одному значення масштабних коефіцієнтів: для кулачкового механізму зі штовхачем, що зворотно-поступально рухається:
)max, Н1 і Н2 і двічі про інтегрував вихідну функцію (мал. 4.3), обчисляють один по одному значення масштабних коефіцієнтів: для кулачкового механізму зі штовхачем, що зворотно-поступально рухається:
mj= 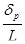 ;
; 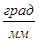 ; ms=
; ms= 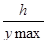 ;
; 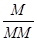 .
.
(4.4)
m 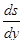 =
=  ;
; 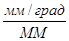 ; m
; m 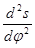 =
= 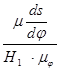 ;
; 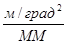
- або для кулачкового механізму з хитним коромислом:
mj= 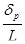 ;
; 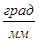 ; mj=
; mj= 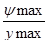 ;
; 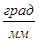 .
.
m 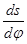 =
= 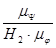 ;
; 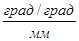 ; m
; m 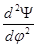 =
= 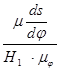 ;
;  . (4.5)
. (4.5)
Знаючи масштаби всіх кінематичних діаграм, визначають значення: пройденого шляху штовхача S=ms-у або рогу повороту коромисла y=mj×у
- швидкості штовхача 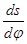 =m
=m 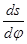 ×у¢; або коромисла
×у¢; або коромисла 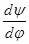 =m
=m 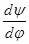 ×у² прискорення штовхача
×у² прискорення штовхача 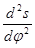 =m
=m 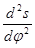 ×у²;
×у²;
- або коромисла 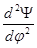 =m
=m 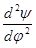
 ×у²;
×у²;
в будь-якому положенні механізму. Ці значення вписують потім у таблицю 4.1.
Таблиця 4.1
Значення переміщень і рогів повороту і їх похідних
| № положення | 1 | 2 | … | і | … | К | |
| S(y) | мм (град) | ||||||
| ds/dj (dy/dj) | м/гр (гр/гр) | ||||||
| D2s/dj2 (d2y/dj2) | м/гр2 (гр/гр2) |
4.4 Динамічний аналіз кулачкового механізму
а) Кулачковий механізм із штовхачем, що зворотно-поступально рухається, (мал.4.1 а)
Для визначення теоретичного початкового радіуса кулачка будують фазовий портрет S- 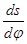 у декартовій системі координат (мал.4.4), для чого з початку координат «О» відкладають нагору відрізок OR, обумовлений ходом штовхача h і довільно прийнятим для цієї побудови масштабним коефіцієнтом ms
у декартовій системі координат (мал.4.4), для чого з початку координат «О» відкладають нагору відрізок OR, обумовлений ходом штовхача h і довільно прийнятим для цієї побудови масштабним коефіцієнтом ms
OR= 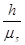 (4.9)
(4.9)
який розмічають від О точками А1... А13 відповідно до графіка S-j на мал. 4.3 в. Через точки А1, А2.Аі відрізка OR проводять перпендикуляри до нього (горизонталі), на яких відкладають відрізки A1L1, A2L2... AіLі, що відповідають значенням передатної функції (аналогу швидкості (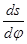 )і) для кожного значення рогу повороту кулачка, j1,j2... jі
)і) для кожного значення рогу повороту кулачка, j1,j2... jі
AіLі= 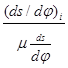 (4.10)
(4.10)
де масштабний коефіцієнт m 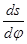 аналога швидкості приймають рівним прийнятому раніше масштабному коефіцієнтуms переміщення, тобто
аналога швидкості приймають рівним прийнятому раніше масштабному коефіцієнтуms переміщення, тобто
m 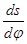 =ms (4.11)
=ms (4.11)
Побудову виконують у правій системі координат. При видаленні штовхача передатну функцію (аналог швидкості 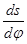 ) вважають позитивної і відкладають управо, а при зближенні (опусканні) штовхача - негативної і відкладають уліво. З'єднуючи плавної кривої (за допомогою лекала) кінці Lі відрізків AіLі одержують замкнуту криву - шуканий фазовий портрет S-
) вважають позитивної і відкладають управо, а при зближенні (опусканні) штовхача - негативної і відкладають уліво. З'єднуючи плавної кривої (за допомогою лекала) кінці Lі відрізків AіLі одержують замкнуту криву - шуканий фазовий портрет S- 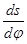 . Під рогом nдоп. до проведеної вертикалі проводять дві дотичні HM і CF до побудованої кривої. Точка O1¢ перетинання цих дотичних визначить положення осі обертання кулачка, що має найменший радіус – вектор romіп.= O1¢О×ms і необхідний у цьому випадку мінімальний ексцентриситет e×=[e]ms. У тому випадку, коли ексцентриситет заданий, проводять вертикаль q-q, усунуту щодо осі ординат S на розмір відрізка [e], що відповідає заданому ексцентриситету e
. Під рогом nдоп. до проведеної вертикалі проводять дві дотичні HM і CF до побудованої кривої. Точка O1¢ перетинання цих дотичних визначить положення осі обертання кулачка, що має найменший радіус – вектор romіп.= O1¢О×ms і необхідний у цьому випадку мінімальний ексцентриситет e×=[e]ms. У тому випадку, коли ексцентриситет заданий, проводять вертикаль q-q, усунуту щодо осі ординат S на розмір відрізка [e], що відповідає заданому ексцентриситету e
[e]= 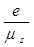 (4.13)
(4.13)
і точка O1 перетинання цієї лінії з дотичної HM визначить найменший для заданих умов теоретичний радіус ro кулачка
ro=O1O×ms (4.14)
 2020-09-26
2020-09-26 171
171








