2020-09-26
163
а) 
б)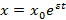 
в)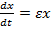 
Уравнение 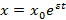– это решение дифференциального уравнения, связывающего скорость изменения численности популяции 
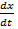с численностью популяции 
.
62. Укажите соответствие (ε – коэффициент роста в модели Мальтуса)
а) 
1) численность особей возрастает
б)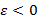 
2) численность особей убывает
в) ε=0 3) численность особей не изменяется
В законах изменения численности популяции, описанных в вопросах 58, 60 и 61, коэффициент ε имеет смысл разницы коэффициентов рождаемости и смертности. Если рождаемость превышает смертность, популяция растет. Если наоборот – вымирает. Если рождаемость равна смертности – популяция стабильна.
63. Пусть начальное число особей равно 10 000. Коэффициент роста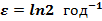 
. Используя модель Мальтуса, рассчитайте количество особей спустя 2 года
а) 20 000
б) 40 000
в) 30 000
г) 100 000
Модель Мальтуса: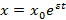
Подставляем 
и t=2
= …
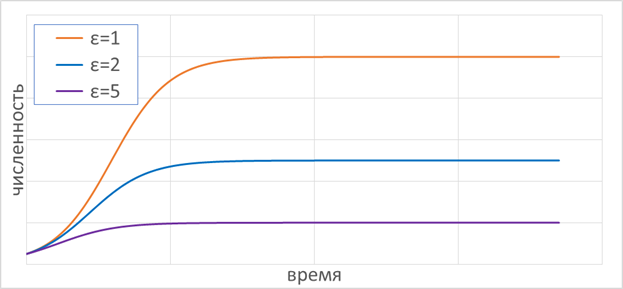
Чем меньше вероятность внутривидовой конкуренции, тем
а) быстрее растет число особей
б) медленнее растет число особей
в) больше стационарное значение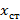 
г) меньше стационарное значение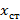
Термин «вероятность внутривидовой конкуренции» некорректен, имелся в виду коэффициент δ члена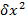 
в дифференциальном уравнении
описывающем скорость изменения численности популяции.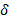 
имеет смысл коэффициента, характеризующего частоту встреч и, соответственно, актов конкуренции особей в популяции.
Численное решение этого уравнения получается таким:
