2020-10-10
114Краткая теория
Дифракцией называется …………...………………………………………………….
……………………………………..…………………….....……………………………..….
Условие наблюдения дифракции: ……………….....……………………………..…
……………………………………..…………………….....……………………………..….
Дифракция Фраунгофера – это ….…………...………………………………………
……………………………………..…………………….....……………………………..….
Одномерная дифракционная решетка - это…………………………………………
……………………………………..…………………….....……………………………..….
……………………………………..…………………….....……………………………..….
Условие наблюдения главных максимумов дифракционной картины:
(5.1)
где
d – ………………………………………………………………………............................................
j – ………………………………………………………………………............................................
λ – ………………………………………………………………………............................................
k – ………………………………………………………………………...........................................
Распределение интенсивности света, получаемое на экране наблюдения после прохождения волны через дифракционную решетку, представлено на рис. 1
|
|
|
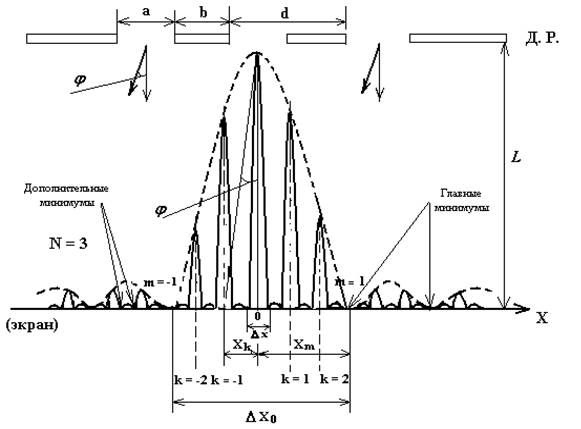
Рис. 1
На рис. 1 пунктирная линия – это ……………………………………………………
……………………………………..…………………….....……………………………..….
Помимо главных максимумов дифракционная картина содержит …………….
……………………………………..…………………….....……………………………..….
……………………………………..…………………….....……………………………..….
Дифракционная решетка позволяет в …….. раз увеличить интенсивность света в области максимумов по сравнению с картиной дифракции
на одной щели.
При выполнении условия L >> d постоянная дифракционной решетки d может быть найдена по формуле:
(5.4)
где
– ……………………………………………………………………….........................................
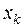L – ………………………………………………………………………............................................
λ – ………………………………………………………………………............................................
k – ………………………………………………………………………............................................
При повороте плоскости решетки относительно плоского фронта падающей волны на угол q появляется дополнительная разность хода волн от щелей решетки. Дифракционная картина изменяется: расстояние между главными максимумами увеличивается. При этом угол дифракции можно вычислять так же, как при нормальном падении света, но с уменьшенным значением периода решетки, который называется ………………………..………………………………………………………………
Эта величина может быть рассчитана по формуле (5.8):
(5.8)
Экспериментальная часть
После настройки оборудования в соответствии с порядком выполнения работы необходимо в выделенной ниже области листа отчета отметить центры главных максимумов первых трех порядков и центрального максимума для каждого угла θ:
|
|
|
q – угол между ……………………………………………………………………………
……………………………………..…………………….....……………………………..….
Обработка результатов измерений
1. Для каждой дифракционной картины миллиметровой линейкой необходимо измерить и записать в соответствующие таблицы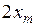 
– расстояние между максимумами 1, 2 и 3 порядков по обе стороны от центрального максимума.
Таблица 1
| θ° | Порядок спектра k | 2 Xk, мм | Xk, мм | d, мкм | < d >, мкм | D d, мкм | e, % |
| 0 | 1 |
|
|
| |||
| 2 | |||||||
| 3 |
Таблица 2
| θ° | Порядок спектра k | 2 Xk, мм | Xk, мм | d’, мкм | < d’>, мкм | Δ d, ’ мкм | ε, % | 
мкм
|
| 30 | 1 |
|
|
|
| |||
| 2 | ||||||||
| 3 | ||||||||
| 60 | 1 |
|
|
|
| |||
| 2 | ||||||||
| 3 |
На лицевой панели установки заданы значения:
L = …………… - ………………………………………………………………………
……………………………………..…………………….....……………………………..….
l = …………… - ………………………………………………………………………
……………………………………..…………………….....……………………………..….
Студент(ка) гр. ____ _________________________________ (указать ФИО)
Дата выполнения _________ Подпись преподавателя _________________
2. По данным табл. 1 рассчитать постоянную дифракционной решетки d для каждого порядка спектра k по формуле (5.4):
d1 =
d2 =
d3 =
3. Вычислить среднее значение постоянной решетки:
< d > =
4. Найти отклонения di от среднего:
Δ d 1 =
Δ d 2 =
Δ d 3 =
5. Найти среднюю квадратичную погрешность
6. Задать надежность α (0,9 или 0,95) и в таблице найти коэффициент Стьюдента
tα = при α =
7. Найти абсолютную погрешность измерения расстояния между щелями:
∆ d = tα·S d =
8. Найти относительную погрешность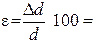 
Результаты занести в таблицу 1.
9. По данным табл. 2 рассчитайте для угла θ = 30° кажущуюся постоянную дифракционной решетки 
для каждого порядка спектра k по формуле (5.4):
=
=
=
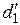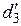10. Вычислить среднее значение кажущейся постоянной решетки:
< > =
11. Найти отклонения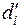 
от среднего:
Δ =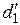
Δ =
Δ =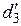
12. Найти среднюю квадратичную погрешность
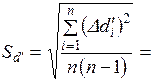
13. Задать надежность α (0,9 или 0,95) и в таблице найти коэффициент Стьюдента
tα = при α =
14. Найти абсолютную погрешность измерения кажущейся постоянной решетки:
∆ = tα·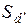 
=
15. Найти относительную погрешность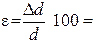 
Результаты занести в таблицу 2.
16. По данным табл. 2 рассчитать для угла θ = 60° кажущуюся постоянную дифракционной решетки 
для каждого порядка спектра k по формуле (5.4):
=
=
=
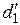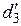17. Вычислить среднее значение кажущейся постоянной решетки:
< 
> =
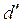18. Найти отклонения 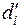от среднего:
Δ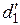 
=
Δ =
Δ =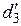
19. Найти среднюю квадратичную погрешность
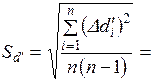
20. Задать надежность α (0,9 или 0,95) и в таблице найти коэффициент Стьюдента
tα = при α =
21. Найти абсолютную погрешность измерения кажущейся постоянной решетки:
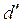∆ = tα·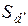 
=
22. Найти относительную погрешность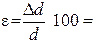
Результаты занести в таблицу 2.
23. По формуле (5.8) вычислить теоретические значения величины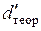 
, подставляя вместо d величину 
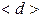– найденное значение постоянной решетки при q = 0°:
при q = 30°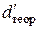 
=
при q = 60° =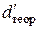
Результаты занести в таблицу 2.
Выводы
Для наблюдения явления ………………………..……………………….... пропустили ……………………..…………………………………………………………………
через …..…………………………………………………………………………………….
На полученной при нормальном падении световой волны ……………………… картине отметили центры …………………………………………………………………. …………………….……………………………….……………………………………….
|
|
|
……………………………………………………………………………………………….
и измерили ………………………………………………………………………………….
……………………………………………………………………………………………….
По полученным данным рассчитали период решетки:
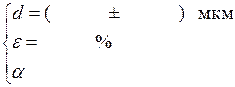
Повторили эксперимент, изменяя ……………………………………………………
……………………………………………………………………………………………….
Провели аналогичные измерения и по полученным данным рассчитали кажущиеся постоянные дифракционной решетки для углов θ 30° и 60°:
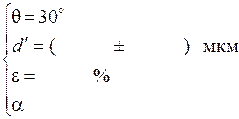
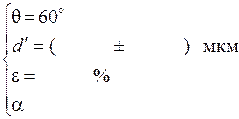
Рассчитали теоретические значения кажущихся постоянных дифракционной решетки:
Экспериментально определенные и теоретически рассчитанные значения кажущихся постоянных решетки при углах θ 30° и 60° (совпадают, совпадают с учетом погрешности измерений, не совпадают – почему – высказать предположение)
……………………………………………………………………………………………….
……………………………………………………………………………………………….
