ИНФОРМАЦИЯ:
è Число А является пределом функции 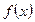 на бесконечности (в бесконечно удаленной точке), если для любого
на бесконечности (в бесконечно удаленной точке), если для любого 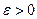 , найдется такое
, найдется такое 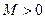 , что при
, что при 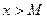 , выполняется неравенство
, выполняется неравенство 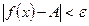 и записывают
и записывают
|
2. Найти пределы функций на бесконечности.
Цель: В процессе выполнения задания закрепить основные навыки в отыскании пределов функции на бесконечности.
21) 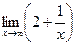 .
.
Решение: Если 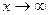 , то функция
, то функция 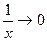 , тогда:
, тогда:
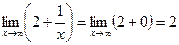 .
.
22) * 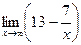
23) * 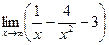
24) 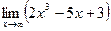 .
.
Решение: Если 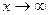 , то функция
, то функция 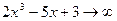 , тогда:
, тогда:
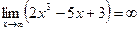 .
.
25) * 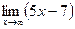 ;
;
26) * 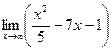
Внимание! Если под знаком предела содержится дробно-рациональная функция, то для того, чтобы найти предел функции необходимо в числителе и знаменателе дроби вынести за скобку х в старшей степени.
27) 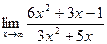
Решение: Данная функция под знаком предела имеет дробно-рациональную функцию. Подставив 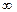 в функцию
в функцию 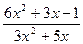 , получим неопределенность
, получим неопределенность 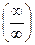 , значит функцию
, значит функцию 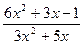 нужно преобразовать. Для этого и в числителе и в знаменателе вынесем за скобку
нужно преобразовать. Для этого и в числителе и в знаменателе вынесем за скобку 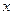 в старшей степени. Старшая степень
в старшей степени. Старшая степень 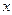 числителя равна 2, знаменателя тоже равна 2. Имеем:
числителя равна 2, знаменателя тоже равна 2. Имеем:
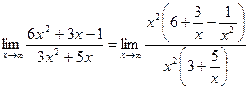
Сократим 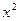 , функции
, функции 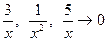 при
при 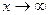 . Учитывая это имеем:
. Учитывая это имеем:
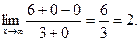

Примечание: Образец оформления в тетради:
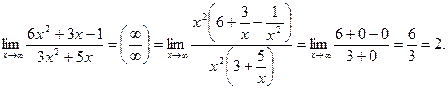
28) * 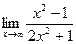
29) * 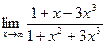
30) 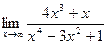 .
.
Решение: Подставив  в функцию
в функцию 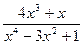 , получим неопределенность
, получим неопределенность 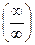 , значит функцию
, значит функцию 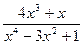 нужно преобразовать. Для этого и в числителе и в знаменателе вынесем за скобку
нужно преобразовать. Для этого и в числителе и в знаменателе вынесем за скобку 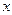 в старшей степени. Старшая степень
в старшей степени. Старшая степень 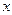 числителя равна 3, знаменателя равна 4. Имеем:
числителя равна 3, знаменателя равна 4. Имеем:
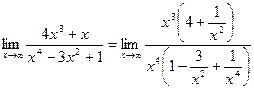
Сократим 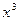 и
и 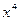 , функции
, функции 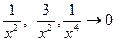 при
при 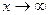 . Учитывая это имеем:
. Учитывая это имеем:
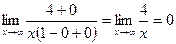 (функция
(функция 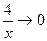 при
при 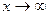 ).
).
31) * 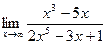
32) 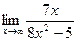
33) 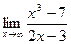
Решение: Подставив  в функцию
в функцию 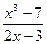 , получим неопределенность
, получим неопределенность 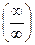 , значит функцию
, значит функцию 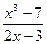 нужно преобразовать. Для этого и в числителе и в знаменателе вынесем за скобку
нужно преобразовать. Для этого и в числителе и в знаменателе вынесем за скобку 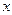 в старшей степени. Старшая степень
в старшей степени. Старшая степень 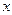 числителя равна 3, знаменателя равна 1. Имеем:
числителя равна 3, знаменателя равна 1. Имеем:
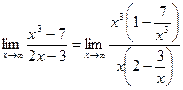
Сократим 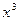 и
и 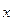 , функции
, функции 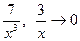 при
при 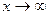 . Учитывая это имеем:
. Учитывая это имеем:
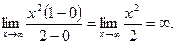
34) * 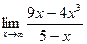 ;
;
35) 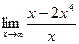 .
.
Раздел 2. Дополнительное задание.
1) Вычислить пределы:
1. 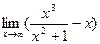
2. 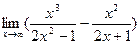
3. 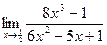 ;
;
4. 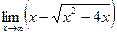 .
.
5. 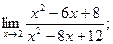
6. 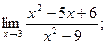
7. 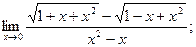
8. 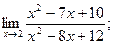
9. 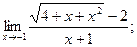
10. 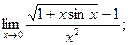
11. 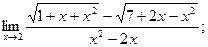
12. 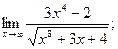
13. 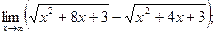
14. 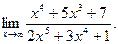
? Домашнее задание:
Вариант
1) Найти пределы функций:
1. 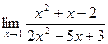 ;
;
2. 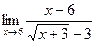 ;
;
3. 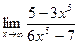 ;
;
4. 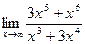 ;
;
5. 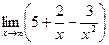 .
.
Вариант
1) Найти пределы функций
1. 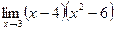
2. 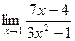 ;
;
3. 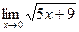 ;
;
4. 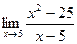
5. 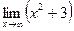
Вариант
1) Найти пределы функций:
1. 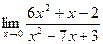 ;
;
2. 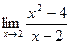 ;
;
3. 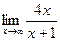 ;
;
4.  ;
;
5. 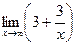 .
.
Вариант
 2020-10-10
2020-10-10 115
115