Предел функции в точке

Практического занятия по № 1

 для студента

Дисциплина: Математика

Специальность: Юрист

Год обучения: 2 курс, 1 семестр

Тема: Теория пределов

 

Разработчик: преподаватель дисциплины «Математика» Л.В. Журавлёва

 

 

 Асино, 2020

 

 

Тема: Теория пределов

Уважаемые студенты!

Теория пределов играет основополагающую роль в математическом анализе, позволяет определить характер поведения функции при заданном изменении аргумента. С помощью предела можно выяснить, имеет ли функция в заданной точке разрыв. Через пределы определяются такие понятия математики как производная, неопределенный и определенный интегралы, составляющие основу дифференциальных уравнений, которые, в свою очередь получили непосредственное применение в медицинской практике. Пределы являются основным средством в построении теории рядов.

Цели занятия

 

Студент должен уметь:

− вычислять пределы функций в точке и на бесконечности;

− раскрывать неопределенности.

 

Студент должен знать:

− место понятия предела в математическом анализе;

− понятие предела функции в точке и на бесконечности;

− теоремы о пределах;

− понятие бесконечно малой, бесконечно большой функции;

− виды неопределенностей, способы их раскрытия;

− замечательные пределы.

 

Материал для повторения: лекция 1,2

Оснащение занятия: дидактический материал

 

 

 

 

 

Практическое занятие №1

 

Тема: Теория пределов.

 Раздел 1. Основное задание.

Пределы и их свойства

 

Предел функции в точке.

 ИНФОРМАЦИЯ:

è Число А является пределом функции 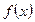 в точке x₀, если для любого 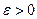, найдется такое , что при , выполняется неравенство  и записывают

è

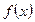Функция  непрерывна в точке x_0, если предел функции в этой точке равен значению функции в этой точке.

è Свойства пределов:

1)

2)

3)

4)

5)

6)

! Все правила имеют смысл, если пределы функци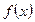й  и существуют.

Внимание: Задания, помеченные звездочкой (*), обязательны для выполнения!

ð Выполнить задания:

 

1. Найти пределы функций в точке.

Цель: В процессе выполнения задания закрепить основные навыки в отыскании пределов функции в точке.

1) .

Решение: В этом пределе в функцию , стоящую под знаком предела подставляем  (т.к. ) и получаем:

 

2) * ;

3) * ;

4) ;

5)

 

6)

Решение: В этом пределе подставим в функцию , получим:

 - получили неопределенность .

Чтобы найти предел этой функции нужно ее преобразовать, обратив внимание, что в числителе данной функции стоит выражение, содержащее корень . Домножим числитель и знаменатель дроби на выражение противоположное (или сопряженное) данному. Это будет выражение . Получим

Выражение, стоящее в числителе свернем по формуле разности квадратов , получим

Сократим  в числителе и знаменателе, и подставим   в функцию, получим

Примечание: Образец оформления в тетради:

 

7) * ;

8) * ;

9) * ;

10) ;

11)

 

 

12)

Решение: Подставив  в функцию   получим неопределенность , значит функцию    нужно преобразовать, разложив числитель на множители по формуле разности квадратов . Имеем:

 

13) *

14)

 

15)

16) .

Решение: Подставив  в функцию   получим неопределенность , значит функцию  нужно преобразовать, разложив числитель и знаменатель на множители.

Для этого решим два квадратных уравнения (общий вид ):

Т.к. , то по теореме Виета найдем корни квадратного уравнения:

И числитель, и знаменатель представляют собой квадратный трехчлен . По формуле разложения квадратного трехчлена на множители  получим:

Подставив полученные разложения в функцию, имеем:

17) * ;

18) * ;

19)

20)