Дана некоторая функция многих переменных f(x1,x2,x3,…..,xn) или 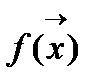 надо найти такое значение
надо найти такое значение 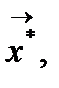 при котором функция
при котором функция  принимает экстремальное значение (минимальное или максимальное). Процесс поиска экстремального значения иногда называют оптимизацией.
принимает экстремальное значение (минимальное или максимальное). Процесс поиска экстремального значения иногда называют оптимизацией. 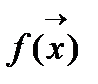 называют оптимизируемой или целевой функцией
называют оптимизируемой или целевой функцией 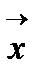 называют вектором параметров оптимизации. В области определения функции может быть несколько экстремумов. Все существующие методы многомерной оптимизации позволяют определить лишь один из экстремумов. Какой именно экстремум будет определён, зависит от выбора начального приближения:
называют вектором параметров оптимизации. В области определения функции может быть несколько экстремумов. Все существующие методы многомерной оптимизации позволяют определить лишь один из экстремумов. Какой именно экстремум будет определён, зависит от выбора начального приближения: 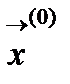 Методы поиска экстремума будем рассматривать относительно случая поиска минимума, для функции двух переменных.
Методы поиска экстремума будем рассматривать относительно случая поиска минимума, для функции двух переменных.
Все методы многомерной оптимизации делятся на два класса: градиентные; безградиентные.
Градиентный метод. Градиентом называется вектор равный сумме произведений частных производных на соответствующие орты. Орта – единичный связанный вектор, направленный вдоль координатной оси.
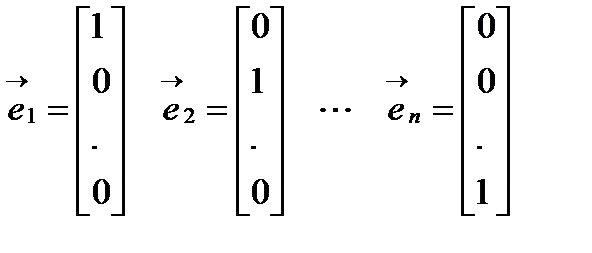
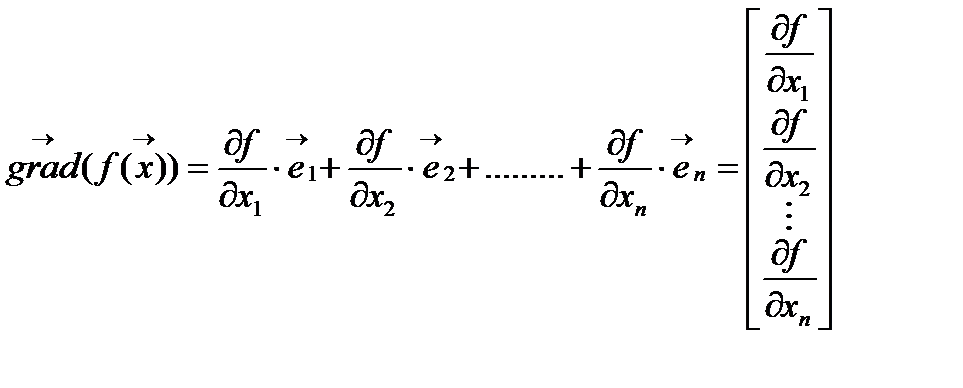 Основные свойства градиента: Норма градиента определяет скорость изменения функции в направление градиента; Градиент всегда направлен в сторону наиболее быстрого возрастания функции, т.е. в этом направлении норма вектора градиента максимальна; Градиент перпендикулярен линии уровня. Антиградиентом называется вектор, направленный в сторону противоположную градиенту.
Основные свойства градиента: Норма градиента определяет скорость изменения функции в направление градиента; Градиент всегда направлен в сторону наиболее быстрого возрастания функции, т.е. в этом направлении норма вектора градиента максимальна; Градиент перпендикулярен линии уровня. Антиградиентом называется вектор, направленный в сторону противоположную градиенту.
Алгоритм
1) Дана функция n переменных 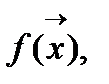 точность ε, параметр шага h, задаем начальное приближение
точность ε, параметр шага h, задаем начальное приближение 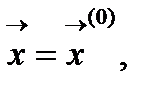 вычисляем значение функции
вычисляем значение функции 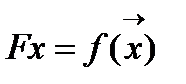
2) Вычисляем вектор градиента 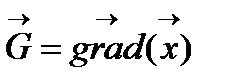 и единичный вектор градиента
и единичный вектор градиента 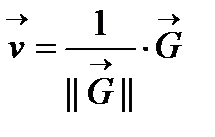
3) Вычисляем новое приближение, делая шаг в направление антиградиента  и вычисляем значение функции
и вычисляем значение функции 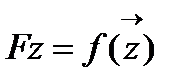
4) Проверяем условие Fz < Fx
5) Если условие выполняется, то за начальное приближение принимаем 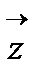 т.е.
т.е.  , переходим на пункт 2.
, переходим на пункт 2.
6) Иначе, проверяем условие окончания h < ε
7) Если условие выполняется, то выводим 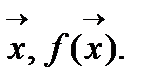 Конец алгоритма
Конец алгоритма
8) Если не выполняется, то уменьшаем параметр шага h=h/3 и переходим на пункт 2

| 
|
|
| |
Программа. Многомерная оптимизация. Градиентный метод.
function DATA
global x0 h eps;
x0=[0.3;0.3];
h=0.5;
eps=0.1;
end
function [ fx ] = f(x)
fx=x(1)^2+x(2)^2-5;
end
function [ G ] = Grad(x)
G=[2*x(1);2*x(2)];
end
function [ x,fx ] = fun_MnogomernOpt_Grad(x0,h,eps)
x=x0;
fx=f(x);
for i=1:100
v=Grad(x)./norm(Grad(x));
z=x-h*v;
fz=f(z);
if fz<fx
x=z;
fx=fz;
else
if abs(h)<eps
i
break;
else
h=h/3;
end %if
end %if
end %for i
end % function
function GLAV_MnogomernOpt_Grad
global x0 h eps x fx;
DATA;
[ x,fx ] = fun_MnogomernOpt_Grad(x0,h,eps);
REPORT;
end % function
function REPORT
global x0 h eps x fx;
disp('Mnogomernaya optimizaciya gradient');
disp(' ');
disp('Arguments');
x0
disp(['h = ' num2str(h,'%10.5f') ]);
disp(['eps = ' num2str(eps,'%10.5f') ]);
disp('Results');
x
disp(['fx = ' num2str(fx,'%10.5f') ]);
end % function
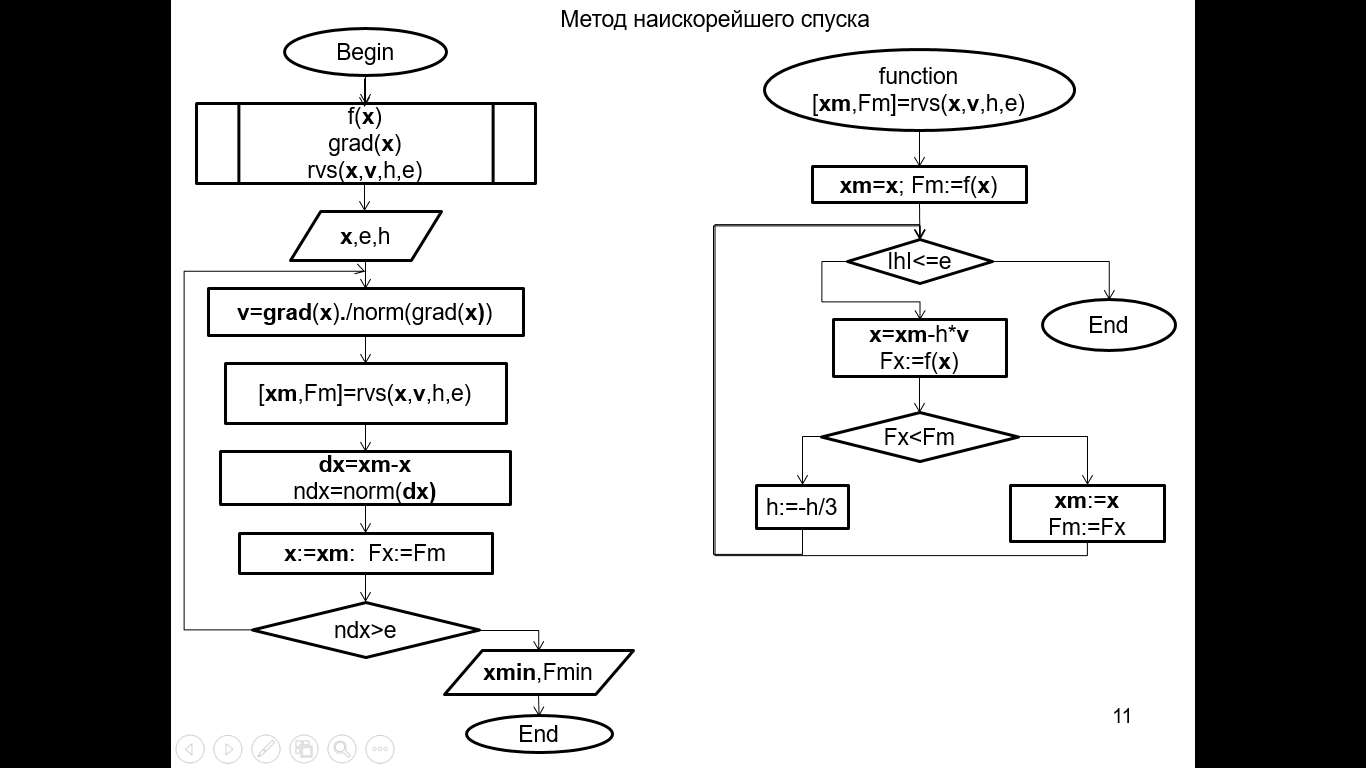
Программа. Многомерная оптимизация. Метод наискорейшего спуска.
function DATA
global x0 h eps;
x0=[0.3;0.3];
h=0.5;
eps=0.1;
end
function [ fx ] = f(x)
fx=x(1)^2+x(2)^2-5;
end
function [ G ] = Grad(x)
G=[2*x(1);2*x(2)];
end
function [ xm,fm ] = rvs(x,v,h,eps)
xm=x;
fm=f(x);
for i=1:100
if abs(h)<=eps
i
break;
else
x=xm-h*v;
fx=f(x);
if fx<fm
xm=x;
fm=fx;
else
h=-h/3;
end %if
end %if
end %for i
end
function [ x,fx ] = fun_MnogomernOpt_NSpusk(x0,h,eps)
x=x0;
for i=1:100
v=Grad(x)./norm(Grad(x));
[ xm,fm ] = rvs(x,v,h,eps);
dx=xm-x;
ndx=norm(dx);
x=xm;
fx=fm;
if ndx<eps
i
break;
end %if
end %for i
end % function
function GLAV_MnogomernOpt_NSpusk
global x0 h eps x fx;
DATA;
[ x,fx ] = fun_MnogomernOpt_NSpusk(x0,h,eps);
REPORT;
end % function
function REPORT
global x0 h eps x fx;
disp('Mnogomernaya optimizaciya naiskor spusk');
disp(' ');
disp('Arguments');
x0
disp(['h = ' num2str(h,'%10.5f') ]);
disp(['eps = ' num2str(eps,'%10.5f') ]);
disp('Results');
x
disp(['fx = ' num2str(fx,'%10.5f') ]);
end % function
| 
|
Симплексный метод. Симплексом в n-мерном пространстве называется выпуклый многоугольник с n+1 вершиной. n=2 треугольник n=3 тетраэдр.
Алгоритм
1) Дана функция 2x переменных 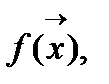 точность ε, параметр h, начальное приближение
точность ε, параметр h, начальное приближение 
2) Вычисляем координаты вершин симплекса
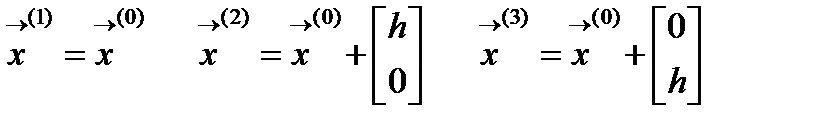
3) Вычисляем значения функции 
4) Определяем (рис.2.10.1) худшую вершину  и координаты отраженной вершины, она будет лежать на прямой исходящей из худшей вершины и проходящей через середину противоположной грани
и координаты отраженной вершины, она будет лежать на прямой исходящей из худшей вершины и проходящей через середину противоположной грани
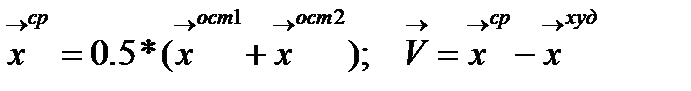
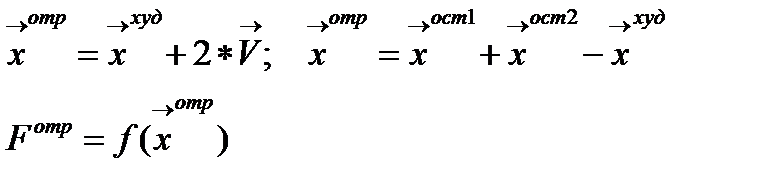
|     
|
 2020-10-10
2020-10-10 168
168








